Mortality Statistics

The Office for National Statistics collects mortality data for the United Kingdom. There's lots of information hidden within the data, but some of it is quite difficult to extract and/or visualise.

The underlying data for questions of life expectancy and mortality rates would seem to be a statistic named "Qx" (raw data). According to their guide, this is defined by the ONS as:

The mortality rate between age x and (x +1); that is, the probability that a person aged x exactly will die before reaching age (x +1).

It is sometimes expressed as a probability multiplied by 100,000. You can plot this for males as a surface with one axis being the age, "x", and the other being the year of observation of "Qx":

The noise towards the "back" of the graph is due to the fact that concrete data beyond the age of 100 is very sparse, so probabilities are difficult to calculate accurately. The next derived value is "Lx" which the ONS defines as:

The number of survivors to exact age x of 100,000 live births of the same sex who are assumed to be subject throughout their lives to the mortality rates experienced in the 3-year period to which the national life table relates.

I've approximated that as a normalised probability:

L[0] = 1

L[i] = L[i-1] * (1 - Q[i-1])

This gives a monotonically decreasing graph that reminds me a bit of a zero curve from fixed-income finance.

You can already see that the shape of the "Lx" curve has changed appreciably between 1850 and 2000. But the graphs (which I prepared using the excellent plotly) become easier to interpret if we add more colour levels:

You can start to see that there are strange "striations" in the surface. We now look at "Dx", defined as:

The number dying between exact age x and (x +1) described similarly to Lx.

I used the following formula:

D[i] = L[i] - L[i+1]

This gives a surface that has a few interesting features clearly visible:

1. The infant mortality rate (defined here as the number of deaths between 0 and 1 years, i.e. D[0]) has dropped from over 15% in 1850 to less than 0.5% after 2000.
2. The adult life expectancy has improved; particularly after about 1950. This is indicated by the increase in height of the hump near the "front" of the surface, along with a gradual shift of the highest point towards greater ages. I suggest this is due to the introduction of the National Heath Service.
3. There is a curious small green hump in the plateau near Year=1918, Age=20.

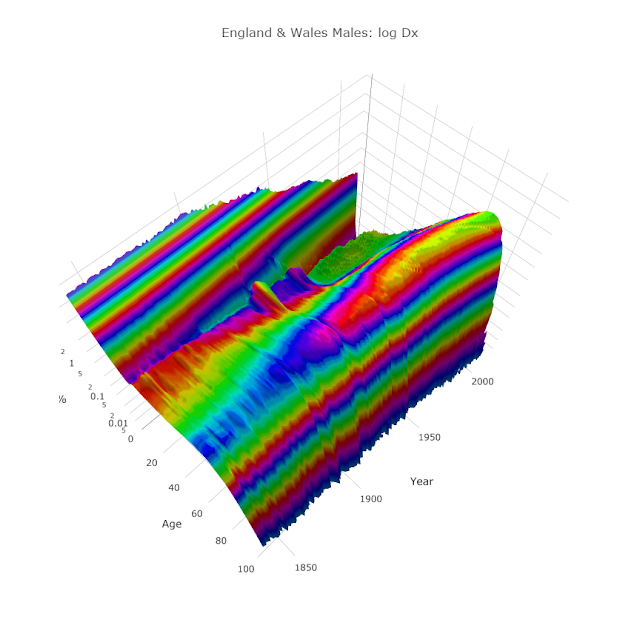
If, instead of graphing "Dx", we graph "log10(Dx)", we see even more features:

We can see that there is a second hump a couple of decades later that the original. Obviously these are due to the two World Wars (1914-1918 and 1939-1945 for Britain). However, the humps are present (though to a lesser extent) in the female graph too:

I was somewhat confused by this but it appears that some UK "life tables" (as actuaries optimistically call them) do not include deaths of service men and women on active duty. So perhaps the humps account for only civilian casualties: e.g. bombing victims and deaths due to general privations caused by the wars.

Another feature I found quite striking was the "male late-teen spike" that is seen better in this view:

There is a relatively sudden increase in male deaths in late-teens. This is well-known phenomenon that is nowhere near as pronounced in the female data:

In fact, after World War II, for females older than one year, log10(Dx) becomes amazingly linear until it peaks at 88 years old (for 2013 data).

One final feature, that I originally thought was a data or plotting bug, is the diagonal cleft you can just see in the green peak to the far right of the male (and female) Dx surfaces:

The diagonal cleft is aligned at exactly forty-five degrees:

Year=2000, Age=81 approx
Year=1950, Age=31 approx
Year=1940, Age=21 approx
Year=1930, Age=11 approx
Year=1920, Age=1 approx

My first theory is that the cleft is due to deaths in World War II. If a large percentage of young people are killed in the space of a few years, then this age range will be "under-represented" in the death statistics in subsequent years.

My second theory involves not the death rate, but the live birth rate. There was a noticeable dip in live births during World War I:

This dip wasn't seen during Second World II. Essentially, if there were fewer babies born in 1917-1919, there will be relatively fewer eight-one-year-olds in the year 2000.

So which theory is correct? I honestly don't know. Perhaps neither, Perhaps both. It may just be due to an accident of history that the drop in birth rate during World War I coincides with the tragic loss of men and women in their early twenties during World War II.

Interactive graphs here. Data courtesy of ONS.

Lexicon 1

For a long time, I've been thinking about implementing a word puzzle dictionary to help solve (or cheat at, if you prefer) crosswords, codewords, Scrabble, and the rest. You know the sort of thing:

"One across, nine letters: C-blank-O-blank-S-blank-blank-R-blank" *

I've always assumed that running this on the client-side in JavaScript would be far too slow. It turns out I was very wrong; if you're careful with your coding, you can get it running in a browser on a low-end tablet or phone with memory and CPU cycles to spare.

My first problem was getting hold of a good lexicon or word list. The obvious avenue to explore was the "official" Scrabble word list used in competitions, but it quickly became apparent that there are at least two such lists:

• The Official Tournament and Club Word List (or, more specifically, "TWL06" for the 2006 version) used in USA, Canada and Thailand ; and
• SOWPODS used just about everywhere else.

These are simply lists of words that are considered "valid"; the former is over 178,000 words and the latter over 267,000 words. They do not contain definitions nor any metadata about the words such as frequency.

In contrast, SCOWL (Spell Checker Oriented Word Lists) contains over 423,000 words with information such as relative frequency and regional variations (American/Canadian/British). Some of the words are suspect (domain-specific abbreviations and bad optical character recognition are two likely sources of suspicious "words") but the frequency information makes it easy to cull outliers.

Instead of choosing just one word list, I decided to go for all three and divided the superset of words into five levels of "rarity" based on the SCOWL frequency metadata. It turns out that SOWPODS is a superset of TWL06, but contains some words not found in SCOWL.

After a lot of curation (in Excel, of all tools!) I ended up with a list of 432,852 words split into five levels of increasing "rarity". Each word is implicitly tagged with the word lists in which it is found. I limited the words to those between two and fifteen letters (inclusive) where each "letter" is one of the twenty-six Roman letters "A" to "Z" (no digits, apostrophes, hyphens or accents are allowed).

I could have stored the lexicon as a simple text file or as a JSON array of strings, but this would have taken up several megabytes, so I decided to have a go at trivial compression. I know, I know ... most HTTP servers will serve up compressed files out of the box and there exist any number of JavaScript libraries that do client-side decompression of ZIP files, but I felt like re-inventing a wheel. Give me a break!

The main constraint I gave myself was to try to get the lexicon to the client-side in a usable form as quickly as possible. This meant a trade-off between file size and time taken to decompress and store in a suitable data structure. One thing you don't want to do is sort half a million words into alphabetical order on the client. That means the lexicon (or parts thereof) needs to be pre-sorted.

Sorted word lists have a lot of redundancy at the beginning of each entry. For example, imagine a list starting like this:

• AARDVARK
• AARDVARKS
• AARDWOLF
• AARDWOLVES
• ...

If we replace the beginning of each word with a digit ('0' to '9') specifying how many letters from the previous word we should replicate, the list becomes:

• 0AARDVARK
• 8S
• 4WOLF
• 7VES
• ...

Another technique is to substitute common letter sequences with ASCII characters outside the ranges '0' to '9' and 'A' to 'Z'. It turns out that the most common four-letter sequences near the end of the words are:

NESS TION ABLE ICAL MENT INGS LESS

For three-letter sequences, the list is:

ING OUS IES ATE TIC TER ISM IST SES INE ION IVE 

While the most common near-end two-letter sequences are:

ED ER ES AL LY AN IC EN IT OR IS ON AR LE IN IA ST ID RA PH UL LA OM IL CH TE CE US UR AT OL

Using these two simple techniques, the 432,852 words can be compressed into a single ASCII string of just over 1.5 million characters. This string can be efficiently converted into a high-performance in-memory data structure within a second on a typical PC.

The full demo can be found here, whilst the JavaScript file that decompresses the word list is lexicond.js.

* "CLOISTERS" obviously