I've just received a very suspicious email from "internethelp@<[-redacted-].com". It purports to be assistance for a query I had with an online service. But I know better! It's just another blatant phishing scam by that master cyber-criminal intern Ethel P.
Monday, 29 March 2021
Friday, 26 March 2021
Colour Pick 1: Goldenrod
As part of my investigation into colour names, I've been writing a lot of JavaScript code to perform colour space transformations.
When I started the colour pick work, I did the "right thing" and refactored all the colour-related functionality into a library. The library is named "goldenrod" after the X11 colour of that name (#DAA520).
 |
| Solidago virgaurea minuta "Dwarf Goldenrod" |
The library is just a plain old bunch of functions and lists organised into three files:
goldenrod.js
This script contains the main entry points exposed as fields of the global object "chilliant.goldenrod". They are primarily conversion functions with signatures of the following form:
float[3] chilliant.goldenrod.{source}_to_{destination}(float value[3])
Above, "{source}" and "{destination}" are colour space tags as listed in the following table:
| Tag | Colour Space | value[0] | value[1] | value[2] |
| sRGB | sRGB | red 0.0 to 1.0 | green 0.0 to 1.0 | blue 0.0 to 1.0 |
| HSV | HSV a.k.a. HSB | hue 0.0 to 360.0 degrees | saturation 0.0 to 1.0 | value 0.0 to 1.0 |
| HSL | HSL | hue 0.0 to 360.0 degrees | saturation 0.0 to 1.0 | lightness 0.0 to 1.0 |
| HWB | HWB | hue 0.0 to 360.0 degrees | whiteness 0.0 to 1.0 | blackness 0.0 to 1.0 |
| CIEXYZ | CIE 1931 XYZ | X 0.0 to 1.0 | Y luminance 0.0 to 1.0 | Z 0.0 to 1.0 |
| CIExyY | CIE 1931 xyY | x 0.0 to 100.0 | y 0.0 to 100.0 | Y luminance 0.0 to 100.0 |
| CIELab | CIE 1976 L*a*b* | L* lightness 0.0 to 100.0 | a* ~ -100.0 to 100.0 | b* ~ -100.0 to 100.0 |
| CIELuv | CIE 1976 L*u*v* | L* lightness 0.0 to 100.0 | u* ~ -200.0 to 200.0 | v* ~ -200.0 to 200.0 |
| CIELChab | CIE 1976 L*C*hab | L* lightness 0.0 to 100.0 | C* chroma ~ 0.0 to 100.0 | hab hue 0.0 to 360.0 degrees |
| CIELChuv | CIE 1976 L*C*huv | L* lightness 0.0 to 100.0 | C* chroma ~ 0.0 to 100.0 | huv hue 0.0 to 360.0 degrees |
Note that for conversions to and from the hexacone colour spaces (HSV/HSL/HWB) the tag "RGB" is used instead of "sRGB" to emphasize the fact that no linearization or delinearization is performed. Thus, the name "chilliant.goldenrod.RGB_to_HSL" is used instead of "chilliant.goldenrod.sRGB_to_HSL".
All conversions assume a standard D65 illuminant with a two-degree observer angle.
At the time of writing, not all permutations of source and destination are directly supported, but it's a trivial change to add the missing "chains".
The additional members of "chilliant.goldenrod" are listed below.
bool chilliant.goldenrod.within_sRGB(any srgb)
A function that returns true if, and only if, 'srgb' is an array of at least three numbers all between 0.0 and 1.0 inclusive.
float[3] chilliant.goldenrod.force_sRGB(any srgb)
Forces 'srgb' to be a valid sRGB triplet with each element between 0.0 and 1.0. If any channel is greater than one, the whole triplet is scaled back. If 'srgb' cannot be interpretted as a valid triplet, black [0,0,0] is returned.
float chilliant.goldenrod.deltaE1994(float ref[3], float lab[3])
Computes the CIELAB ΔE*(1994) colour difference between the two CIEL*a*b* colours. Note that this metric is not symmetric.
float chilliant.goldenrod.deltaE2000(float ref[3], float lab[3])
Computes the CIELAB ΔE*(2000) colour difference between the two CIEL*a*b* colours.
string chilliant.goldenrod.sRGB_to_HEX(float srgb[])
Converts the sRGB triplet (or quartet with alpha) 'srgb' to a hexadecimal colour in the form "#rrggbb" or "#rrggbbaa".
float[3] chilliant.goldenrod.HEX_to_sRGB(string hex)
Converts an hexadecimal colour string in the form "#rgb", "#rgba", "#rrggbb" or "#rrggbbaa" into an sRGB triplet. Any alpha component is ignored.
string chilliant.goldenrod.version
util.js
This script contains the guts of the functionality of goldenrod exposed as members of the object "chilliant.goldenrod.util". A large portion is based on the formulae outlined on Bruce Lindbloom's excellent site and should be fairly self-explanatory.
data.js
This script contains useful datasets exposed as members of the object "chilliant.goldenrod.data".
float[][] chilliant.goldenrod.data.cie1931_xyy
The CIE 1931 2-degree chromaticity xyY coordinates from UCL Colour & Vision Research Laboratory. The columns are:
- Wavelength in nm,
- CIE xyY x-ordinate,
- CIE xyY y-ordinate, and
- CIE xyY Y luminance.
object[] chilliant.goldenrod.data.css4
The CSS 4 colour names taken from Mozilla.
any[] chilliant.goldenrod.data.centore
The 267 ISCC-NBS centroids from Paul Centore's site in index order. The columns are:
- Name (string),
- Munsell colour (string),
- Red (int),
- Green (int),
- Blue (int),
- sRGB hexadecimal (string).
Note that seven of the centroids are outside the sRGB gamut so are missing the final four columns. It would be nice to have the out-of-gamut values for red/green/blue because those points could still be matched via (for instance) Euclidean distance searchers. However, I have been unable to recreate Paul's methodology to fill in the blanks.
object chilliant.goldenrod.data.cns
A 627-entry map between the Color Naming System and sRGB values in the form:
{"black": {hex: "#000000", srgb: [0,0,0]},..."yellowish orange": {hex: "#CC9333", srgb: [0.8,0.575,0.2]}}
This is a "best guess" at the values based on "A New Color-Naming System for Graphics Languages".
See "generateCNS()" for details.
any[] chilliant.goldenrod.data.iscc
The 260 ISCC-NBS centroids from "data.centore" that are within the sRGB gamut, formatted like "data.cns".
See "generateISCC()" for details.
Unit Tests
Tuesday, 23 March 2021
HSL and CIELCh(ab) Hue Wheels
I've been looking at colour pickers recently and came across (what I think is) an interesting cul-de-sac.
HSL colour pickers often have a hue wheel similar to this one from Paint Shop Pro 5 (1998):
 |
| Paint Shop Pro 5 colour picker dialog |
The wheel is rendered as an angle sweeps from 0 to 360 degrees clockwise:
output = HSL_to_RGB(angle, 100%, 50%)
The HSL wheel looks like this:
 |
| HSL hue wheel |
Note that the "hue" components of HSL, HSV and HWB are identical. However, this is not the case for the cylindrical version of CIE Lab, a.k.a. CIELCh(ab).
We can construct the CIELCh(ab) hue wheel as follows:
rgb = CIELChab_to_sRGB(70, 30, angle)
hsl = RGB_to_HSL(rgb)
output = HSL_to_RGB(hsl.h, 100%, 50%)
We choose a CIE perceptual lightness (L*) of 70 and chroma (C*) of 30 so as not to go out-of-gamut when converting to sRGB. We also implicitly assume the reference white to be the CIE standard illuminant D65 and a 2-degree observer angle.
We use HSL to fully saturate the output colour to produce the following wheel:
 |
| CIELCh(ab) hue wheel |
Note that the colours have shifted somewhat. This becomes clear if we plot both wheels on the same chart:
 |
| HSL (outer) and CIELCh(ab) (inner) hue wheels |
There's already an excellent comparison of these two wheels by Elle Stone, so I won't go into that here.
For reasons that will hopefully become clear in a later post, what I really wanted to do was plot the CIELCh(ab) hue wheel efficiently in WebGL. Who wouldn't?
I coded "CIELChab_to_sRGB" et al in GLSL (more on that later too) but felt a bit queasy performing such complicated arithmetic, particularly when the results get shunted through an RGB-HSL-RGB hack at the end. There must be an efficient way of translating CIELCh(ab) hue to HSL hue, surely?
If we plot the relationship, we get:
 |
| CIELCh(ab) hue versus HSL hue |
I looks like a fairly linear albeit wavy relationship, doesn't it? So let's plot the difference modulo 360 degrees:
 |
| Difference in hues modulo 360 degrees |
It now looks fairly sinusoidal, so maybe we can approximate it with the sum of a few sine waves.
If the input is the CIELCh(ab) hue angle in degrees and the desired output is the HSL hue, we can write:
output = input + c + a0*sin(b0+input) + a1*sin(b1+2*input) + a2*sin(b2+3*input) + …
It turns out you only need four sine terms to get a good approximation and Microsoft Excel Solver is more that capable of finding appropriate values for the offset "c", scale factors "a0" to "a3" and phase shifts "b0" to "b3".
I initially coded the formula as a GLSL function that takes the hues in the range zero to one, like so:
float hstar2hue(float input) {// Convert CLIELCh(ab) hue [0..1] to HSV/HSL/HWB hue [0..1]float a0 = 0.011681489;float a1 = -0.053365543;float a2 = -0.00331377;float a3 = -0.009398634;float b0 = -0.527823872;float b1 = -1.606202694;float b2 = 1.054897946;float b3 = 0.102411421;float c = 0.91047088;float output = input + c;output += a0 * sin(b0 + input * 2.0 * 3.1415926536);output += a1 * sin(b1 + input * 4.0 * 3.1415926536);output += a2 * sin(b2 + input * 6.0 * 3.1415926536);output += a3 * sin(b3 + input * 8.0 * 3.1415926536);return mod(output, 1.0);}
But we can take advantage of GLSL's SIMD nature and get:
float hstar2hue(float input) {// Convert CLIELCh(ab) hue [0..1] to HSV/HSL/HWB hue [0..1]vec4 a = vec4(0.011681489, -0.053365543, -0.00331377, -0.009398634);vec4 b = vec4(-0.527823872, -1.606202694, 1.054897946, 0.102411421);float c = 0.91047088;vec4 v = sin(vec4(1.0, 2.0, 3.0, 4.0) * input * 6.28318530718 + b);return mod(input + dot(a, v) + c, 1.0);}
It's then just a question of converting the HSL-style hue to RGB:
vec3 hue2rgb(float h) {float r = abs(h * 6.0 - 3.0) - 1.0;float g = 2.0 - abs(h * 6.0 - 2.0);float b = 2.0 - abs(h * 6.0 - 4.0);return clamp(vec3(r, g, b), 0.0, 1.0);}
And we've got all the ingredients for a fragment shader to render the CIELCh(ab) hue wheel.
I'll leave it as an exercise for the reader to work out the reverse HSL-to-CIELCh(ab) hue approximation as well as those for CIELCh(uv).
Friday, 5 March 2021
Colour Names 5
Still more colour naming experiments...
My experiments with HWB-51 last time divided up the whiteness-blackness plane for a particular hue (e.g. blue) like this:
 |
| Partitioning the whiteness-blackness plane in HWB-51 |
It can be seen that the partitioning doesn't occur in native whiteness-blackness space. Here's the relevant JavaScript pseudo-code:
var hwb_w = Math.min(linear_r, linear_g, linear_b);
var hwb_b = 1 - Math.max(linear_r, linear_g, linear_b);
var p = hwb_w + hwb_b;
var q = hwb_w / p;
if (p < 0.125) {
return "vivid " + name;
}
if (p < 0.375) {
return name;
}
if (p >= 0.875) {
return achromatic(q);
}
...
Above, "p" is the Manhattan distance from the vivid corner; a measure of "achromicity". And "q" is a measure of how much of the "achromicity" is white, as opposed to black.
We compare this with the computation of HSV saturation and value parameters:
var hsv_v = Math.max(linear_r, linear_g, linear_b);
var chroma = hsv_v - Math.min(linear_r, linear_g, linear_b);
var hsv_s = (hsv_v > 0) ? (chroma / hsv_v) : 0;
...
We see that there are obvious similarities:
p == 1 - chroma
== 1 - hsv_s * hsv_v
and
q == (hsv_v - chroma) / (1 - chroma)
== hsv_v * (1 - hsv_s) / (1 - hsv_s * hsv_v)
This shouldn't be a complete surprise as Smith and Lyons themselves noted that the "HWB model is very closely related to the HSV model". So we could quite simply reformulate the HWB-51 rules to use HSV or, indeed, HSL.
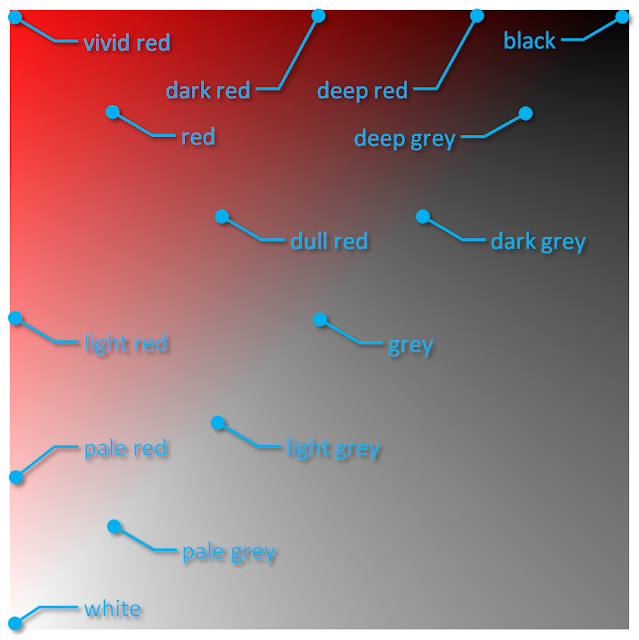
However, one of the reasons for the creation of HWB in 1995 was to have a "more intuitive hue-based color model" and I quite like the symmetry in the whiteness-blackness plane:
- Adding whiteness creates a tint (base → light → pale → white)
- Adding blackness creates a shade (base → dark → deep → black)
- Adding both creates a tone (base → dull → grey)
NOTE: Don't forget that HWB assumes that red, green and blue channels are linear. So sRGB values need linearizing, that is [and this was a new phrase for me] "inverse companding".
Colour Names 4
Even more colour naming experiments...
I added conversions for the ISCC-NBS System of Color Designation (1939 onwards) based on Paul Centore's centroids. I was unable to reproduce Paul's results, so I cannot fill in the seven blanks for out-of-sRGB-gamut points:
- brilliant orange (4.5YR8.0/12.1)
- vivid orange yellow (9.0YR7.2/16)
- deep olive green (5.0GY2.0/8.0)
- deep green (6.0G2.3/9.1)
- deep bluish green (4.5BG2.3/9.0) and
- deep greenish blue (4.5B2.5/9.0)
The "extrapolated" sRGB centroids could still be useful when searching for colour names but need to be computed from the original Munsell data points. This is a fiendish problem that I hope to re-visit if and when I implement a colour library in Egg.
To improve upon the ad hoc naming scheme of ISCC-NBS, the Color Naming Scheme (CNS) (1982) sought to systematize the name construction. CNS produces a palette of 627 colours, some of which have rather ambiguous names:
- very dark vivid yellowish brown
- very light grayish bluish purple
It does, however, encompass the majority of the eleven basic colour terms:
- white
- black
- red
- green
- yellow
- blue
- brown
- purple
- pink
- orange
- grey
All but "pink" are included, though "brown" is somewhat shoe-horned in.
As pointed out elsewhere, CNS doesn't seem to have a reference implementation, so it's very difficult to judge results. I've implemented a simple HSL centroid scheme pending further information.
Thinking about the basic colour terms (and grating against the use of terms like "chartreuse"), I implemented HWB-51 as a cut-down version of HWB-51 but just using the eleven basic terms plus the following adjectives:
- deep
- dark
- light
- pale
- vivid
- dull
This produces 77 combinations, but only 55 are used as names ("vivid black" is not meaningful):
| black | - | - | - | - | - | - |
| grey | deep grey | dark grey | light grey | pale grey | - | - |
| white | - | - | - | - | - | - |
| pink* | - | - | light pink* | - | - | dull pink |
| red | deep red | dark red | light red* | pale red* | vivid red | dull red |
| orange | deep orange* | dark orange* | light orange | pale orange | vivid orange | dull orange |
| brown* | - | dark brown* | - | - | - | dull brown |
| yellow | deep yellow | dark yellow | light yellow | pale yellow | vivid yellow | dull yellow |
| green | deep green | dark green | light green | pale green | vivid green | dull green |
| blue | deep blue | dark blue | light blue | pale blue | vivid blue | dull blue |
| purple | deep purple | dark purple | light purple | pale purple | vivid purple | dull purple |
There are four pairs of synonyms:
- "pink" = "light red"
- "light pink" = "pale red"
- "brown" = "dark orange"
- "dark brown" = "deep orange"
This makes a total of 51 unique colours. Unfortunately, there's a large gap in the hue wheel between green and blue where cyan usually sits:
 |
| Hue ranges for HWB-51 names |
Perhaps turquoise could be added.
The light/dark split for orange/brown and pink/red works quite well in HWB:
 |
| Approximate partitioning of whiteness-darkness plane for HWB-51 (orange/brown) |
We could extend the idea to all sectors of the hue wheel:
- red → pink/red
- orange → orange/brown
- yellow → yellow/olive
- green → lime/green
- blue → blue/navy
- purple → violet/purple
However, now we're drifting away from using basic colour terms.
As an example of the various naming schemes, here are the results of looking up the web-safe colour "#FFCCFF":
| X11 | Thistle | 9.5 |
| RGB-125 | chantilly | 3.4 |
| RGB-64 | mauve | 8.7 |
| RGB-27 | orchid | 17.0 |
| ISCC-NBS | purplish white | 0.1 |
| CNS | very light strong purple | 1.4 |
| HSL-79 | white | - |
| HSV-79 | dull magenta | - |
| HWB-51 | pale purple | - |
| HWB-91 | pale magenta | - |
The final column is the ΔE*(2000) distance metric.
This is an extreme example because every name is different!
Monday, 1 March 2021
Colour Names 3
Some more colour naming experiments...
After creating the RGB-125 palette (one-word names for colours based on five levels each of red, green and blue), I limited the number of levels to 64 (4x4x4). This is similar to the EGA source palette.
The EGA palette uses the adjective "bright" to describe colours with any channel at 100% intensity. This idea is mirrored in the "vivid" modifier of the ISCC-NBS system and Color Naming System. I thought that "bright" could be confused with "light", so I chose "vivid" as the prefix for any RGB-64 colour that has maximal chroma.
RGB-64 has 39 base colour names ("amaranth", "amber", "apple", "aquamarine", "azure", "black", "blue", "bluebell", "brown", "celeste", "cerise", "cerulean", "chartreuse", "cyan", "denim", "erin", "green", "grey", "harlequin", "inchworm", "jade", "liberty", "magenta", "mauve", "milan", "mint", "olive", "orange", "orchid", "pink", "plum", "poison", "purple", "red", "spring", "tradewind", "violet", "white" and "yellow") and 3 modifiers ("dark", "light" and "vivid"). The bold names correspond to the eleven (contentious) basic colour terms.
RGB-27 is a strict subset of RGB-125 covering 3x3x3 colour points. Unfortunately, we lose "brown" and "pink" in the process.
At this point, I turned my attention to limited, hue-based colour naming schemes.
HSL-79 is a scheme based on the HSL colour space. The hue (an angle between 0 and 360 degrees) is split into 12 equal segments:
- red
- orange
- yellow
- chartreuse
- green
- spring
- cyan
- azure
- blue
- violet
- magenta
- rose
- deep (very low lightness)
- dark (low lightness)
- light (high lightness)
- pale (very high lightness)
- dull (low saturation)
- black
- deep grey
- dark grey
- grey
- light grey
- pale grey
- white
HSV-79 is similar but based on the HSV colour space instead of HSL. I tried to parameterize the partitioning of the segment so that each contains approximately the same number of RGB (256x256x256) colour points.
 |
| HWB-91 reference points for a given hue (x-axis is blackness, y-axis is whiteness) |
The numbers in the final column are the ΔE*(2000) colour differences between "#FFCCFF" and the nearest colour from the discrete palette.

