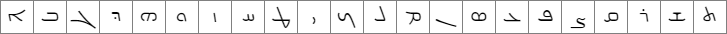Unicode Trivia U+09F8

Codepoint: U+09F8 "BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR"
Block: U+0980..09FF "Bengali"

Decimal Day. 15 February 1971. A Monday. The day the United Kingdom and the Republic of Ireland converted to decimal currency. Before that, each pound was divided into twenty shillings and each shilling into twelve pence. We'll ignore farthings.

So, if I bought something worth one penny with an old, pre-decimalisation five pound note, I'd get a dirty look and the following change:

£4 19/11 = £4. 19s. 11d = 4 pounds, 19 shillings, 11 pence

Such mixed-radix currencies were not uncommon. In British India, the rupee had been divided into sixteen annas, each anna into four pice (paisa), and each pice into three pies. The change from five rupees for a one pie item would be:

Rs. 4/15/3/2 = 4 rupees, 15 annas, 3 pice, 2 pies

In pre-decimal Bengal, the taka (rupee) had been divided into sixteen ana, and each ana into twenty ganda. The change from five taka for a one ganda item would be:

Tk. 4/15/19 = 4 taka, 15 ana, 19 ganda

Of course, that's in English using the Latin script and Western Arabic numerals. In Bengali, one could have written:

৪৲৸৶৹৻১৯

U+09EA U+09F2 U+09F8 U+09F6 U+09F9 U+09FB U+09E7 U+09EF

As Anshuman Pandey, points out, only one currency mark was actually used when multiple units were written. We'll return to this in due course, but in the meantime I've left that refinement out of the example above.

Bengali is a Brahmic script written left-to-right, so in Unicode this example is:

1. U+09EA "BENGALI DIGIT FOUR"
2. U+09F2 "BENGALI RUPEE MARK"
3. U+09F8 "BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR"
4. U+09F6 "BENGALI CURRENCY NUMERATOR THREE"
5. U+09F9 "BENGALI CURRENCY DENOMINATOR SIXTEEN"
6. U+09FB "BENGALI GANDA MARK"
7. U+09E7 "BENGALI DIGIT ONE"
8. U+09EF "BENGALI DIGIT NINE"

The first two glyphs ("৪৲") represent "4 taka" in decimal; the Bengali digit four just happens to look like a Western Arabic digit eight. The next three glyphs ("৸৶৹") represent "15 ana". This is complicated by the fact that, traditionally, ana were written as fractions of a taka. Finally, the last three glyphs ("৻১৯") represent "19 ganda" in decimal where, just to confuse us further, the ganda mark comes before the digits, not after them as with taka and ana.

The ana component is the most perplexing. The Unicode codepoint name for U+09F8, "BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR", doesn't really help. Fortunately, there's an explanation within the much later proposal to add the ganda mark in 2007.

The fifteen possible quantities of ana are:

• ৴৹ = 1 ana (Numerator 1)
• ৵৹ = 2 ana (Numerator 2)
• ৶৹ = 3 ana (Numerator 3)
• ৷৹ = 4 ana (Numerator 4)
• ৷৴৹ = 5 ana
• ৷৵৹ = 6 ana
• ৷৶৹ = 7 ana
• ৷৷৹ = 8 ana
• ৷৷৴৹ = 9 ana
• ৷৷৵৹ = 10 ana
• ৷৷৶৹ = 11 ana
• ৸৹ = 12 ana (Numerator One Less Than the Denominator)
• ৸৴৹ = 13 ana
• ৸৵৹ = 14 ana
• ৸৶৹ = 15 ana

This looks like a modified base-4 tally mark system. But, thinking back to what Anshuman Pandey said about elided currency marks, I wonder if this scheme didn't originate in a finer-grained positional system.

Imagine that instead of the taka being divided directly into sixteen ana, it was divided into four virtual "beta", which were themselves divided into four virtual "alpha". Obviously:

• ana = alpha + beta * 4

But now we have the following encoding:

• ৴ = 1 alpha (Numerator 1)
• ৵ = 2 alpha (Numerator 2)
• ৶ = 3 alpha (Numerator 3)
• ৷ = 1 beta
• ৷৷ = 2 beta
• ৸ = 3 beta (Numerator One Less Than the Denominator)

For beta, the "denominator" is indeed four, to the mysterious U+09F8 "BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR" suddenly makes sense.

We can now come up with an algorithm for writing out a currency amount according to the scheme described by Anshuman Pandey:

• Let T, A, G be the number of taka (0 or more), ana (0 to 15), ganda (0 to 19) respectively
• If T is not zero then
• Write out the Bengali decimal representation of T
• If both A and G are zero
• Write out U+09F2 "BENGALI RUPEE MARK"
• We're finished
• Let α be A modulo 4 (0 to 3)
• Let β be A divided by 4, rounded down (0 to 3)
• If β is 1, write out U+09F7 "BENGALI CURRENCY NUMERATOR FOUR"
• If β is 2, write out U+09F7 "BENGALI CURRENCY NUMERATOR FOUR" twice
• If β is 3, write out U+09F8 "BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR"
• If α is 1, write out U+09F4 "BENGALI CURRENCY NUMERATOR ONE"
• If α is 2, write out U+09F5 "BENGALI CURRENCY NUMERATOR TWO"
• If α is 3, write out U+09F6 "BENGALI CURRENCY NUMERATOR THREE"
• If G is zero then
• Write out U+09F9 "BENGALI CURRENCY DENOMINATOR SIXTEEN"
• We're finished
• Write out U+09FB "BENGALI GANDA MARK"
• Write out the Bengali decimal representation of G
• We're finished

For our example, T=4, A=15, G=19, α=3, β=3 and the output is:

৪৸৶৻১৯

U+09EA U+09F8 U+09F6 U+09FB U+09E7 U+09EF

This representation is surprisingly concise and totally unambiguous.

Unicode Trivial U+0950

Codepoint: U+0950 "DEVANAGARI OM"
Block: U+0900..097F "Devanagari"

Next, we come to our first Brahmic script: Devanagari. Devanagari is the most widely-used Brahmic script. Almost 50% of the Indian population use it to write their native language. It is a left-to-right abugida used to write dozens of languages.

It is sometimes glibly called a "washing line" script because, unlike Latin/Greek/Cyrillic scripts that "sit" on top of their baselines, Devanagari also "hangs" from a head line:

Devanagari script
देवनागरी लिपि

Devanagari typography is non-trivial, even when the letterforms are isolated:

Devanagari Type Anatomy [source]

Of course, anthropomorphism in typography isn't limited to Brahmic scripts, but one can take "type anatomy" quite literally:

Design Parameters of Devanagari (Gokhale, 1983) [source]

The flipside of grammatology is phonology.

"Om" is the sound of a sacred spiritual symbol in Indic religions. In Devanagari, in its simplest form, it is written:

Om
ओम
U+0913 U+092E

However, there is also a ligatured codepoint in the Devanagari block named "DEVANAGARI OM":

Om (sign)
ॐ

U+0950

There are currently many Oms encoded into Unicode. The Devanagari Om was added right at the onset in Unicode 1.0 (1991). This incorporated a wholesale import of the ISCII (Indian Script Code for Information Interchange, 1988) character sets which encode Om as a multi-byte sequence (0xA1 0xE9).  The Unicode Consortium allocated U+0950 "DEVANAGARI OM" to allow one-to-one mapping of ISCII on this basis. Of course, once you allow one Om through...

Unicode Trivia U+08C8

Codepoint: U+08C8 "ARABIC LETTER GRAF"
Block: U+08A0..08FF "Arabic Extended-A"

Unicode blocks are not allocated sequentially. Consequently, "Arabic Extended-A" (U+08A0..08FF, originating in Unicode 6.1, January 2012) comes numerically after "Arabic Extended-B" (U+0870..089F, originating in Unicode 14.0, September 2021).

Even more confusing, codepoints within a block can be allocated at different times. For example, U+08C8 "ARABIC LETTER GRAF" was assigned in Unicode 14.0 (September 2021); but its neighbour, U+08C7 "ARABIC LETTER LAM WITH SMALL ARABIC LETTER TAH ABOVE" was assigned in Unicode 13.0 (March 2020).

U+08C8 "ARABIC LETTER GRAF" is an addition to the Arabic script for writing the Balti language:

Isolated form of U+08C8 [source]

For example, the Balti word for knife (U+08C8 U+06CC):

[source]

U+08C8 is the only specific addition required for the Arabic script to be able to write Balti, although two other codepoints (U+0F6B "TIBETAN LETTER KKA" and U+0F6C "TIBETAN LETTER RRA", added in Unicode 5.1, April 2008) are needed to write Balti using the Tibetan script.

Balti is spoken in Baltistan, or Little Tibet, a mountainous region in the Gilgit-Baltistan part of Pakistan-administered Kashmir. This may be the origins of the balti curry dish popular in the UK since the nineteen-seventies.

Unicode Trivia U+0891

Codepoint: U+0891 "ARABIC PIASTRE MARK ABOVE"
Block: U+0870..089F "Arabic Extended-B"

Consider this photograph by Tinou Bao:

Fruit Seller
"The guy asked to be photographed"

It could elicit any number of reactions:

1. What wonderfully colourful fruit!
2. Are those dates expensive?
3. I hope he doesn't drop cigarette ash on that fruit
4. His fruit are suspiciously glossy
5. Why did he want his photo taken?
6. That's an interesting symbol above the price

You're in the right place if your reaction was number six.

That symbol, circled in blue, is an Arabic supertending currency symbol for Egyptian piastres. The photo was used as part of the proposal for the addition of two new currency codepoints:

• U+0890 "ARABIC POUND MARK ABOVE"
• U+0891 "ARABIC PIASTRE MARK ABOVE"

The proposal was formally submitted in August 2020, accepted in October 2020 and released as part of Unicode 14.0 in September 2021.

[source]

Unicode Trivia U+0861

Codepoint: U+0861 "SYRIAC LETTER MALAYALAM JA"
Block: U+0860..086F "Syriac Supplement"

The Syriac Supplement block contains letters used for writing Suriyani Malayalam, also known as Syriac Malayalam. This is an Eastern Syriac script with eleven new letters added to capture Malayalam sounds:

The Syriac and Malayalam scripts are almost entirely unrelated; the former is a right-to-left abjad from the Middle East:

Whilst the latter is a left-to-right abugida from Southern Asia:

So the "mashing together" of the two scripts is somewhat surprising and problematic.

For example, the Suriyani Malayalam letter "ja" only appears in isolated form, so the "standard" U+0D1C "MALAYALAM LETTER JA" could have been used, however, the decision was taken to encode a separate U+0861 "SYRIAC LETTER MALAYALAM JA":

Although it may be possible to use U+0D1C within a Syriac environment, a separate encoding is needed [...] so that Syriac vowel marks can be combined with the letter. Furthermore the differing directionalities of the Malayalam and Syriac scripts may cause problems for introducing a Malayalam character directly in Syriac sequences.

Anyone who has tried editing text with mixed left-to-right and right-to-left script will appreciate that last comment.

Suriyani Malayalam is used by Saint Thomas Christians of Kerala in India as a liturgical language. According to tradition, Thomas the Apostle voyaged to Muziris on the Malabar coast (Kerala) in 52 CE, bringing Christianity to the region. This may sound implausible, but Kerala had an established Jewish community at around that time, particular in Cochin. So it is possible for an Aramaic-speaking Jew, such as Saint Thomas from Galilee, to make a trip to Kerala via the maritime Silk Road routes:

[source]

Perhaps not surprisingly, after almost two thousand years, the Saint Thomas Christians have experienced schisms and (sadly fewer) reunifications:

[source]

Unicode Trivia U+0840

Codepoint: U+0840 "MANDAIC LETTER HALQA"
Block: U+0840..085F "Mandaic"

The Mandaic alphabet contains 22 letters (in the same order as the Aramaic alphabet) and one digraph:

The alphabet is "rounded up" to a symbolic count of 24 letters by repeating the first letter, U+0840 "MANDAIC LETTER HALQA". It is unusual for a Semitic script in being a true alphabet with letters for both consonants and vowels:

1. U+0840 "Halqa" = a [vowel]
2. U+0841 "Ab" = ba
3. U+0842 "Ag" = ga
4. U+0843 "Ad" = da
5. U+0844 "Ah" = ha
6. U+0845 "Ushenna" = wa [vowel]
7. U+0846 "Az" = za
8. U+0847 "It" = eh
9. U+0848 "Att" = ṭa
10. U+0849 "Aksa" = ya [vowel]
11. U+084A "Ak" = ka
12. U+084B "Al" = la
13. U+084C "Am" = ma
14. U+084D "An" = na
15. U+084E "As" = sa
16. U+084F "In" = e [vowel]
17. U+0850 "Ap" = pa
18. U+0851 "Asz" = ṣa
19. U+0852 "Aq" = qa
20. U+0853 "Ar" = ra
21. U+0854 "Ash" = ša
22. U+0855 "At" = ta
23. U+0856 "Dushenna" = ḏ

The eighteenth letter was renamed from "Ass" to "Asz" as part of the original proposal, presumably to stop the giggling at the back of the classroom.

The Classical Mandaic language is still used by Mandaean priests in liturgical rites. It is estimated that there are about 5,500 native speakers. Neo-Mandaic is a modern evolution of Mandaic but generally unwritten. Only a few hundred Mandaeans, located mainly in Iran, speak Neo-Mandaic as a first language.

One of the unintended consequences of the 2003 invasion of Iraq was the diaspora of over 60,000 Iraqi Mandaeans. Today, Sweden has the largest community of any country.

Unicode Trivia U+0837

Codepoint: U+0837 "SAMARITAN PUNCTUATION MELODIC QITSA"
Block: U+0800..083F "Samaritan"

The Samaritan script was derived from the Paleo-Hebrew circa 600 BCE and was used alongside the Aramaic script in Judaism until the latter was repurposed as the Hebrew alphabet circa 100 BCE.

Samaritan is a right-to-left abjad with 22 basic consonants and diacritics to mark vowels:

Much is made of the extensive punctuation in the Samaritan script. Here are the fifteen codepoints of the "Punctuation" column (U+0830 to U+083E):

Unicode Trivia U+07C1

Codepoint: U+07C1 "NKO DIGIT ONE"
Block: U+07C0..07FF "NKo"

As reported by Dr Dianne White Oyler in "A Cultural Revolution in Africa: Literacy in the Republic of Guinea since Independence" (2001), the N'Ko script was developed by Souleymane Kanté in 1949, partly in response to

a 1944 challenge posed by the Lebanese journalist Kamal Marwa in an Arabic-language publication, Nahnu fi Afrikiya [We Are in Africa]. Marwa argued that Africans were inferior because they possessed no indigenous written form of communication. His statement that "African voices [languages] are like those of the birds, impossible to transcribe" reflected the prevailing views of many colonial Europeans. Although the journalist acknowledged that the Vai had created a syllabary, he discounted its cultural relevancy because he deemed it incomplete. [Page 588]

Kanté discarded both Arabic and Latin scripts as unable to transcribe all the characteristics of the Mande languages. Having developed a completely novel alphabet instead,

he called together children and illiterates and asked them to draw a line in the dirt; he noticed that seven out of ten drew the line from right to left. For that reason he chose a right-to-left orientation. In all Mande languages the pronoun n- means "I" and the verb ko represents the verb "to say". [Page 589]

So "N'Ko" means "I say" in all the target languages.

The right-to-left mantra extends not only to words, but to digits and numbers too. The ten digits zero to nine (U+07C0 "NKO DIGIT ZERO" to U+07C9 "NKO DIGIT NINE") face right:

N'Ko digits (top), Western Arabic (middle), Eastern Arabic (bottom)

This is particularly noticeable with U+07C1 "NKO DIGIT ONE": '߁'

Not only that, but the least significant digits of multi-digit N'Ko numbers are on the left, unlike almost all other writing systems. Latin, Greek, Arabic and Hebrew numbers place the least significant digit on the right, even though the latter two scripts are written right-to-left.

Consider the improbable phrase "There are 12345 eggs":

There are 12345 eggs = English

Υπάρχουν 12345 αυγά = Greek

 يوجد ١٢٣٤٥ بيضة = Arabic

יש 12345 ביצים = Hebrew

߁߂߃߄߅ ߞߟߌ߫ ߦߋ߫ ߦߋ߲߬ = N’Ko

In case of tofu:

Note that the order of the codepoints for "1", "2", "3" "4" and "5" occur in ascending memory order in all cases. For example:

At first, I wasn't sure how much "support" the Unicode standard gives for this type of anomaly. UCD's sister project CLDR (Common Locale Data Repository) has very little to say about N'Ko. There is scope for algorithmic number formatting, but I didn't find anything specific.

However, after a bit of thought I realised that, because directionality is a property of each codepoint and not of the script of the codepoints, digit ordering in N'Ko works "out of the box".

Consider these bidirectional class fields ("bc") from the UCD:

• Latin
• "A" (U+0041 "LATIN CAPTIAL LETTER A") =  "L" = strong left-to-right
• "1" (U+0041 "LATIN CAPTIAL LETTER A") = "EN" = European number (left-to-right)
• Greek
• "α" (U+03B1 "GREEK SMALL LETTER ALPHA") =  "L" = strong left-to-right
• Arabic
• "ا" (U+0627 "ARABIC LETTER ALEF") = "AL" =  Arabic letter (right-to-left)
• "١" (U+0661 "ARABIC-INDIC DIGIT ONE") = "AN" =  Arabic number (left-to-right)
• Hebrew
• "א" (U+05D0 "HEBREW LETTER ALEF") = "R" = strong right-to-left
• N'Ko
• "ߊ" (U+07CA "NKO LETTER A") = "R" = strong right-to-left
• "߁" (U+07C1 "NKO DIGIT ONE") = "R" = strong right-to-left

Unlike the other digits, N'Ko digits are marked as strongly right-to-left. The only other examples in Unicode 14.0 I could find were Adlam digits (1989).

Another interesting codepoint from the Unicode "NKo" block is U+07F7 "NKO SYMBOL GBAKURUNEN":

It's a decorative punctuation symbol used to mark the end of a major section of text and represents the three stones holding a cooking pot over a fire:

[source]

Finally, there can't be many alphabets that have their own day: April 14.

[Many thanks to Coleman Donaldson for help with the N'Ko language]

Unicode Trivia U+0780

Codepoint: U+0780 "THAANA LETTER HAA"
Block: U+0780..07BF "Thaana"

The Thaana script is used to write the Maldivian language. According to Wikipedia, it's an abugida with no inherent vowel. According to the ISO standard, it's a right-to-left-written alphabet (as indicated by the hundreds digit of its numeric ISO-15924 code "170").

It first appeared in about 1705 CE and seems have been developed with obfuscation in mind. The alphabet order is arbitrary and the consonant letterforms are derived from numeric figures:

On the top row, in white, are the 24 basic consonants in Thaana alphabetical order. These are the 24 consecutive Unicode codepoints U+0780 "THAANA LETTER HAA" to U+0797 "THAANA LETTER CHAVIYANI".

The second row shows the Arabic-Indic digits one to nine in blue and the Dhives Akuru digits one to six in red. Dhives Akuru was a Maldivian script used before Thaana. The main part of the alphabet looks very much like a simple replacement cipher.

An early version of the Thaana script, Gabulhi Thaana, was written scriptio continua, that is, without inter-word spacing or punctuation. This sounds like an absolute nightmare but was quite common in classical Greek and Latin. Before mechanical printing, Arabic was also written without spacing. This is, perhaps, why many writing systems have distinct letterforms for final letters in words.

According to "Scripts of Maldives", the early Thaana script, Gabulhi Thaana, got its name from the Maldivian word "gabulhi" meaning the in-between stage of a coconut, when it is neither fully ripe nor quite tender. Hence the idea of "immature" or "not fully-formed".

Unicode Trivia U+0753

Codepoint: U+0753 "ARABIC LETTER BEH WITH THREE DOTS POINTING UPWARDS BELOW AND TWO DOTS ABOVE"
Block: U+0750..077F "Arabic Supplement"

Syriac is not the only script that makes extensive use of diacritics. The spread of the Arabic script throughout the world means it is used for diverse languages, many of which have sounds not found in Arabic. Part of the "Arabic Supplement" block contains a column "Extended Arabic letters" with the annotation:

These are primarily used in Arabic-script orthographies of African languages.

One codepoint, U+0753, has the somewhat precise name of "ARABIC LETTER BEH WITH THREE DOTS POINTING UPWARDS BELOW AND TWO DOTS ABOVE". When I render that codepoint using "Noto Sans Arabic" on my PC, I get this:

Noto Sans Arabic (2.004)

When I render it with a default local font, I get:

Arial (7.00)

Spot the difference!

There's definitely a discrepancy in the orientation of the lower dots, but which is correct? I came up with three possibilities:

1. I have old/corrupt font files installed on my PC
2. The name of the Unicode codepoint is incorrect
3. The orientation of the lower dots doesn't really matter, so there is no issue
4. One of the font glyphs is incorrect

Initially, I did indeed think it was an old version of Noto Sans Arabic installed on my machine. But I updated my local version of Noto Sans Arabic to 2.009 with the same results. Google web font specimens confirmed the issue is with Noto Sans Arabic in general:

Three of the four specimens suggest the name of the Unicode codepoint is probably correct. I checked that there are no similarly-named codepoints; there is no "ARABIC LETTER BEH WITH THREE DOTS POINTING DOWNWARDS BELOW AND TWO DOTS ABOVE"

I couldn't really imagine that, carefully named as it is, the orientation of the lower dots in U+0753 was unimportant.

I then checked Unicode Updates and Errata but found no references to this or nearby codepoints.

So the finger of suspicion fell on the glyph within the Noto Sans Arabic font being incorrect. FontForge confirmed this:

I looked through the issues reported for Noto fonts, but found nothing, so I submitted a new one.

Of course, this has only a passing connection to the Unicode standard. But one can easily imagine the amount of noise that has to be ploughed through by the committee along the lines of "My text doesn't get displayed how I expected" just to get to genuine issues with the Unicode standard itself.

According to Wiktionary, U+0753 "ARABIC LETTER BEH WITH THREE DOTS POINTING UPWARDS BELOW AND TWO DOTS ABOVE" is

The third letter of the Hausa alphabet in ajami script, equivalent to Latin script c.

I was initially a bit suspicious of this. Both Omniglot and Wikipedia suggest that the three dots go above that letter, making it more like U+062B "ARABIC LETTER THEH". However, Richard Ishida points out that there are lots of subtle local variations and the initial Unicode proposal shows an "ARABIC LETTER BEH WITH THREE DOTS POINTING UPWARDS BELOW AND TWO DOTS ABOVE" in Figure 5. The proposal cites "Using Arabic Script in Writing the Languages of the Peoples of Muslim Africa" (1992) by Mohamed Chtatou:

"Figure 5" (Chtatou, 1992)

Richard Ishida again:

Unicode policy for the Arabic script is to encode fully precomposed characters rather than to use combining characters for ijam.

It would appear that the task of supporting more obscure and/or infrequent Arabic script glyphs in Unicode (and in fonts) can only get harder.

Unicode Trivia U+0740

Codepoint: U+0740 "SYRIAC FEMININE DOT"
Block: U+0700..074F "Syriac"

Syriac has got to be one of the dottiest scripts in Unicode. The fact that there's a 232-page book devoted to Syriac diacritics says a lot:

[source]

The dot is used for everything in Syriac from tense to gender, number, and pronunciation, and unsurprisingly represents one of the biggest obstacles to learning the language.

Section 9.3 of the Core Specification 14.0.0 gives an introduction to some of these complexities. Within the sub-section concerning exceptions to the diabolical diacritical rules, is this:

The feminine dot is usually placed to the left of a final taw.

This refers to codepoint U+0740 "SYRIAC FEMININE DOT". According to Richard Ishida, this non-spacing mark:

[...] is a feminine marker used with "ܬ" [U+072C SYRIAC LETTER TAW] to indicate a feminine suffix. East Syriac fonts should render as two dots below the base letter, whereas West Syriac fonts render as a single dot to the left of the base.

So far as I can tell, this is the only diacritic currently in Unicode that distinguishes (or elucidates) the underlying word's gender.

Below are variations of "ܩܛܠܬ" (= kill) distinguished solely by diacritics ("ܩ̇ܛܠܬ", "ܩܛ̣ܠܬ" and "ܩܛܠܬ݀") rendered with "Noto Sans Syriac":

Notice U+0740 "SYRIAC FEMININE DOT" at the end (left) of the last line.

[Thanks to Richard Ishida and, indirectly, J F Coakley at Jericho Press]

Unicode Trivia U+0640

Codepoint: U+0640 "ARABIC TATWEEL"
Block: U+0600..06FF "Arabic"

The FIFA World Cup Qatar 2022 logo applies kashida to the Latin script word for "Qatar":

[source]

This is the elongation of the connection between the "t" and "a". In Unicode, U+0640 "ARABIC TATWEEL" (alias "kashida") can be used to represent this elongation. Tatweels are usually only used in Arabic (or similar) scripts, so it's a nice cross-cultural reference in this context.

Here's an extreme example in the form of an Arabic script basmala:

[source]

Tatweels could be considered typographical formatting, but, because a tatweel character was part of ISO/IEC 8859-6 at position 0xE0, it was "inherited" by Unicode as a separate graphical codepoint.

Arabic tatweels are similar to Latin hyphens when used for text justification, but the rules are obviously very different. An excellent history of the topic is given by Titus Nemeth.

[At this point, my complete lack of understanding of Arabic will shine through. Apologies.]

Like its Unicode block-neighbour Hebrew, Arabic script is a right-to-left abjad. The name "Qatar" in Arabic is made up of three Arabic consonants:

• U+0642 "ARABIC LETTER QAF"
• U+0637 "ARABIC LETTER TAH"
• U+0631 "ARABIC LETTER REH"

قطر

If, as part of text justification or for aesthetic effect, we want to widen the word, we could insert a tatweel between the tah and reh:

قطـر

In fact, we can add more tatweels in sequence:

قطـــــر

This is, of course, an artificial example; words of only three consonants are rarely stretched.

Straight line tatweels are not the only mechanism that can be used to justify Arabic text. Others include:

1. Whitespace
2. Letterform lengthening/shortening
3. Ligature variation

Unicode Trivia U+05D0

Codepoint: U+05D0 "HEBREW LETTER ALEF"
Block: U+0590..05FF "Hebrew"

Hebrew is usually written in an abjad script, right-to-left. Abjads are also known as consonant alphabets because they lack "letters" for vowel sounds. Diacritics indicating vowels are used for poetry, religious texts and teaching Hebrew.

When we type the 22 consonants, "alef" (U+0590) to "taw" (U+05EA), a text renderer should render them right-to-left:

But how does it know that?

Within the UCD fields for U+05D0, we see:

bc = R

This means that the "bidirectionality class" for U+05D0 is "any strong right-to-left (non-Arabic-type) character" (UAX #44). This, together with the fiendishly complex bidirectional algorithm (UAX #9), allows text renderers to render arbitrary sequences of mixed-script codepoints correctly.

The U+05D0 "HEBREW LETTER ALEF" codepoint is marked as Hebrew script:

sc = Hebr

but the Unicode bidirectional algorithm does not rely on script-level properties. That is, Unicode says that "alef" is usually rendered "right-to-left", not that "alef" is part of the "Hebrew" script and the "Hebrew" script is usually rendered "right-to-left".

There is no concept of lowercase and uppercase letters in Hebrew; the script is unicameral.

Finally, and appropriately, four Hebrew letters have "final forms" when they appear at the end of words:

This is similar to Greek sigma, but without the special-case handling necessary to overcome the lack of an uppercase final sigma.

Unicode Trivia U+058D

Codepoint: U+058D "RIGHT-FACING ARMENIAN ETERNITY SIGN"
Block: U+0500..058F "Armenian"

The Armenian alphabet was devised in about 405 CE by Mesrop Maštoc' to give Armenians access to Christian texts. It was probably developed from the Greek alphabet with influences from Syriac and possibly Ge'ez scripts. It has uppercase and lowercase letterforms:

Armenian is written with quite distinctive punctuation. See Section 7.6 of the Unicode Core Specification.

Before Unicode, Armenian script was encoded in one of a set of ASCII-like character encodings called ArmSCII. In all three main variants of ArmSCII, there is a slot for the Armenian eternity symbol. The sign comes in two versions; right- and left-facing:

Right- and left-facing Armenian eternity signs [source]

According to Michael Everson:

The Armenian Eternity Sign is the ancient national symbol of Armenia. Its glyph may have either a clockwise or an anti-clockwise orientation, which is composed with curves running from the centre of the symbol. Typically, the sign has eight such curves, a number which symbolizes revival, rebirth, and recurrence. 

The sign is known to be distinguished with both right and left rotations, which represent (more or less) activity and passivity, similarly to the svаsti sign used in Hinduism and Buddhism.

Personally, I find the "left- and right-facing" nomenclature somewhat confusing, but it made it into the Unicode standard:

֍ U+058D "RIGHT-FACING ARMENIAN ETERNITY SIGN"

֎ U+058E "LEFT-FACING ARMENIAN ETERNITY SIGN"

The latter codepoint has an annotation saying it "maps to AST 34.005:1997" which is ArmSCII-7.

The fact that two codepoints were to be added to Unicode (even though only one existed in ArmSCII) was the topic of some debate within the Unicode committee around 2010, along with where to actually place the two codepoints: either the "Armenian" block (the winner!) or "Miscellaneous Pictographic Symbols".

A similar discussion was had about the placement of the Armenian currency sign, dram (U+058F). It could have been placed in the "Currency Symbols" block, but it was positioned at the end of the "Armenian" block because it is "similar to the Armenian letter D" (section 7.1.1).

Unicode Trivia U+051C

Codepoint: U+051C "CYRILLIC CAPITAL LETTER WE"
Block: U+0500..052F "Cyrillic Supplement"

Cyrillic is a script, not an alphabet. There are many alphabets in the Cyrillic script for different languages.

The Kurdish language is usually written today using a Latin-based alphabet (Celadet Alî Bedirxan, 1932) or a modified Perso-Arabic alphabet (Sa’id Kaban Sedqi, 1928). In the past, a Cyrillic alphabet (Heciyê Cindî, 1946) was also used:

Аа Бб Вв Гг Г’г’ Дд Ее Әә Ә’ә’ Жж Зз Ии Йй Кк К’к’ Лл Мм Нн Оо Ӧӧ Пп П’п’ Рр Р’р’ Сс Тт Т’т’ Уу Фф Хх Һһ Һ’һ’ Чч Ч’ч’ Шш Щщ Ьь Ээ Ԛԛ Ԝԝ

The last two letters are not the Latin letters Q and W, they are the Kurdish Cyrillic letters Qa and We:

• 'Ԛ' (U+051A "CYRILLIC CAPITAL LETTER QA")
• 'ԛ' (U+051B "CYRILLIC SMALL LETTER QA")
• 'Ԝ' (U+051C "CYRILLIC CAPITAL LETTER WE")
• 'ԝ' (U+051D "CYRILLIC SMALL LETTER WE")

They were added to the "standard" Cyrillic alphabet to capture Kurdish sounds not found elsewhere.

Cyrillic We (U+051C) is a homoglyph of Latin W (U+0057), and vice versa. In Unicode parlance, they are "confusable".

[source]

Of course, Cyrillic We and Latin W are semantically different letters, even though they may look identical. The Unicode standard deals primarily with codepoints and not their visual representation, so having two distinct codepoints in this case makes sense. Other examples in the Unicode repertoire are less clear-cut.

There is a serious side to Unicode homoglyphs: there is a very real technology security threat associated with them. For this reason, the the Unicode Consortium publishes a partial list of confusables with every release, along with mitigation guidelines.

Unicode Trivia U+047C

Codepoint: U+047C "CYRILLIC CAPITAL LETTER OMEGA WITH TITLO"
Block: U+0400..04FF "Cyrillic"

It is perhaps not surprising, given the history of writing, that there are so many references to religious aspects of letterforms in the Unicode standard. Take U+047C "CYRILLIC CAPITAL LETTER OMEGA WITH TITLO" as an example:

Taken from Unicode Cyrillic Chart

It sits in the "Historic letters" column of the "Cyrillic" block. A look at the official Unicode charts reveals the following annotations:

• [alias] Cyrillic "beautiful omega"
• [note] despite its name, this character does not have a titlo, nor is it composed of an omega plus a diacritic
• [see also] A64C Ꙍ cyrillic capital letter broad omega

Apparently, this glyph (or something that looks similar) is used in Church Slavonic religious texts for the interjection "Oh!" However, there has been some discussion within the Unicode community about this codepoint and its lowercase version:

These characters were originally encoded in the Unicode standard with an erroneous name and representation. After the UTC ruling on Everson et al. (2006), the representation was corrected and an annotation was added to U+047C, reading “despite its name, this character does not have a titlo, nor is it composed of an omega plus a diacritic”. However, no annotation was added to the lowercase form U+047D.

The character that is encoded here is a ligature of the Cyrillic broad (or wide) Omega (encoded at U+A64C and U+A64D) and the ‘great apostrof’, a stylized diacritical mark consisting of the soft breathing (encoded at U+0486) and the Cyrillic kamora (encoded at U+0311). The broad Omega (U+A64D) can occur by itself, without this diacritical mark, in pre-1700 printed Church Slavic books, though not in modern liturgical texts. Functionally, the character with the diacritical mark is analogous to the Greek character ὦ, which also consists of an Omega, a soft breathing mark and a Perispomene. Both the Greek and Church Slavic characters have identical functions: to record the exclamation ‘Oh!’ Since U+047C and U+047D were encoded without a canonical decomposition, though they are linguistically decomposable, they should not be decomposed to avoid an encoding ambiguity. However, in our opinion, the annotation as written does not make this clear.

There has been a suggestion to rename (or alias) U+047C to "CYRILLIC LETTER BROAD OH" with the observation:

In addition, the Unicode note “beautiful omega” should refer to A64C, not to this character.

At the time of writing there are no name aliases in the UCD for any of these codepoints.

It all goes to show that:

1. Naming codepoints is a perilous task.
2. The complexity of the competing interests makes errors inevitable.
3. If mistakes are made, the Unicode stability policy makes fixing them difficult or unappealing.
4. Unicode annotations can be more revealing than the raw UCD data.

Unicode Trivia U+03C2

Codepoint: U+03C2 "GREEK SMALL LETTER FINAL SIGMA"
Block: U+0370..03FF "Greek and Coptic"

The modern lowercase (minuscule) Greek alphabet is encoded in the Unicode range U+03B1 to U+03C9  in the "Greek and Coptic" block:

αβγδεζηθικλμνξοπρςστυφχψω

The uppercase versions of these letters are in the range U+0391 to U+03A9:

ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡ΢ΣΤΥΦΧΨΩ

Tofu alert! Something nasty happens between the capitals rho "Ρ" and sigma "Σ". Here are those ranges rendered in a table:

The grey square is U+03A2: a "reserved" codepoint. This character is also reserved in earlier character sets (e.g. ISO/IEC 8859-7 of 1987) so it's not an anomaly of Unicode. It's the gap where "GREEK CAPITAL LETTER FINAL SIGMA" would sit if it actually existed.

Consider the titlecase Greek word for "Stasis":

Στασις

If we convert this to uppercase by using the following in the Chrome browser's console

"Στασις".toUpperCase()

we get

'ΣΤΑΣΙΣ'

as expected. All three sigmas (initial "Σ", medial "σ" and final "ς") get mapped to capital sigma "Σ":

ΣΤΑΣΙΣ

The UCD lowercase mapping of U+03A3 "GREEK CAPITAL LETTER SIGMA" only mentions U+03C3 "GREEK SMALL LETTER SIGMA". So one would think (like I naively did) that converting "ΣΤΑΣΙΣ" to lowercase would produce

στασισ

but if we use the browser console again

"ΣΤΑΣΙΣ".toLowerCase()

we actually get

'στασις'

(with a final sigma) which is correct but pleasantly unexpected.

The official reason the string mapping is correct is that final sigmas are "special" according to the Unicode standard. There's a file in the UCD named SpecialCasing.txt. Below is the relevant snippet from that text file:

# Special case for final form of sigma

03A3; 03C2; 03A3; 03A3; Final_Sigma; # GREEK CAPITAL LETTER SIGMA

This rule kicks in when the "Final_Sigma" condition is true independent of language.

In reality, every implementation of a lowercase mapping function must have special logic to handle final sigmas. Seriously.

As an example, here's the relevant functionality from the Chrome browser source code: 

// Really special case 1: upper case sigma.  This letter

// converts to two different lower case sigmas depending on

// whether or not it occurs at the end of a word.

if (next != 0 && Letter::Is(next)) {

  result[0] = 0x03C3;

} else {

  result[0] = 0x03C2;

}

This is a gotcha that's obviously bitten people more than once. Even the Unicode Consortium acknowledges it's a can of wormς

Unicode Trivial U+030C

Codepoint: U+030C "COMBINING CARON"
Block: U+0300..036F "Combining Diacritical Marks"

Imagine the role of Bjorn in a heavy metal ABBA tribute band (really?) who styles his name:

Bǰörn

There's a caron over the "j" and a (heavy metal) umlaut over the "o". That's five Unicode codepoints:

U+0042, U+01F0, U+00F6, U+0072, U+006E

When his name is converted to all uppercase for the tour poster:

BJ̌ÖRN

it mysteriously becomes six Unicode codepoints:

U+0042, U+004A, U+030C, U+00D6, U+0052, U+004E

This is because although Unicode has the codepoint U+01F0 "LATIN SMALL LETTER J WITH CARON", it has no single codepoint for "LATIN CAPITAL LETTER J WITH CARON". The case mapping algorithm uses data from the UCD to map U+01F0 to the pair U+004A/U+030C.

U+030C is the codepoint for "COMBINING CARON".

If we convert the name back to titlecase, we get:

Bǰörn

This looks the same (hopefully) but is also made up of six codepoints:

U+0042, U+006A, U+030C, U+00F6, U+0072, U+006E

The "O WITH DIAERESIS" round-tripped okay, but not the "J WITH CARON". What's going on?

Case mapping and case folding are very knotty problems. There are plenty of edge-cases in Unicode where converting to/from uppercase/lowercase and back again does not produce the original input. You cannot perform case-insensitive matching by simply converting both strings to uppercase and comparing for equality. Nor does converting to lowercase (or titlecase) work either.

If we look at the UCD entry for U+01F0 "LATIN SMALL LETTER J WITH CARON", we see:

1. dm = 006A 030C
2. uc = 004A 030C
3. lc = #
4. tc = 004A 030C
5. cf = 006A 030C

This can be interpreted as:

1. The "Decomposition Mapping" is "U+006A U+030C". That's lowercase "j" followed by a combining caron.
2. The (non-simple) "Uppercase Mapping" is "U+004A U+030C". That's uppercase "J" followed by a combining caron.
3. The (non-simple) "Lowercase Mapping" is the unaltered codepoint, i.e. "U+01F0". That's the single codepoint "LATIN SMALL LETTER J WITH CARON".
4. The (non-simple) "Titlecase Mapping" is "U+004A U+030C". That's uppercase "J" followed by a combining caron.
5. The (non-simple) "Case Folding" is "U+006A U+030C". That's lowercase "j" followed by a combining caron.

From these definitions, one can imagine algorithms for:

1. Decomposing strings into normalized forms (NFC/NFD/NFKC/NFKD) to avoid ambiguity, although there are still lots of additional complications.
2. Converting strings to uppercase.
3. Converting strings to lowercase.
4. Converting strings to titlecase.
5. Comparing strings in a case-insensitive way.

Further complications occur when more than one diacritic is attached to a letter. And then there's the question of ordering (collating) text with diacritics...

Perhaps Bjorn was so busy wondering why there's no umlaut in "umlaut" that he missed a trick. He should have styled himself:

U+0243, U+01F0, U+00F6, U+1E5D, U+00F1