Universe 5: Font Detection

Any Unicode codepoint browser ends up as an exercise in font wrangling. Universe is no exception.

The threat of fingerprinting means a browser script cannot typically enumerate the locally installed fonts. There is also currently no native way of determining if a font supports a particular codepoint. One would think that determining font support for codepoints would therefore be problematic, but it turns out to be relatively easy for our use-case with Chrome.

Consider the following JavaScript snippet:

var canvas = document.createElement("canvas");

var context = canvas.getContext("2d");
context.font = "10px font-a,font-b,font-c";
var measure = context.measureText(text);

If a character in the "text" string is not supported by "font-a", Chrome text rendering falls back to using "font-b". If "font-b" also doesn't support the character, "font-c" is used. If the character is not supported by "font-c" either, a system default is used.

We can take advantage of this fall back mechanism by using a "blank" font that guarantees to render any glyph as zero-width/zero-mark. Fortunately, there's just such a font already out there: Adobe Blank:

@font-face {
  font-family: "blank";
  src: url("https://raw.githubusercontent.com/adobe-fonts/
         adobe-blank/master/AdobeBlank.otf.woff") format("woff");
}

Now, we can write a function to test a font for supported characters:

function IsBlank(font, text) {

  var canvas = document.createElement("canvas");

  var context = canvas.getContext("2d");

  context.font = `10px "${font}",blank`;

  var measure = context.measureText(text);

  return (measure.width <= 0) &&

    (measure.actualBoundingBoxRight <= -measure.actualBoundingBoxLeft);

}

The actual code in universe.js has some optimisations and additional features; see "MeasureTextContext()" and "TextIsBlank()".

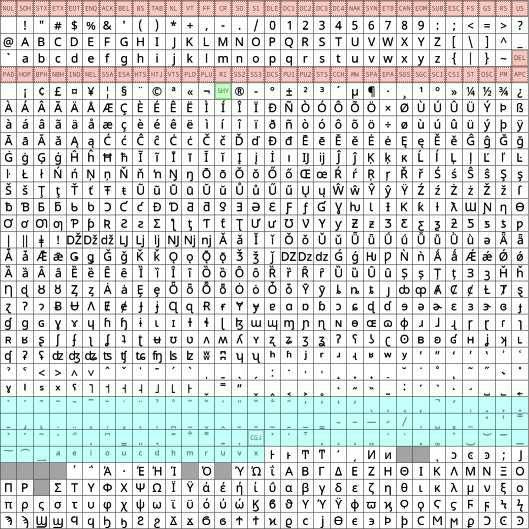
Using this technique, we can iterate around some "well-known" fonts and render them where appropriate. For our example of codepoint U+0040:

The origins of each of the glyphs above are:

1. "notoverse" is the 32-by-32 pixel bitmap glyph described previously.
2. "(default)" is the default font used for this codepoint by Chrome. In my case, it's "Times New Roman".
3. "(sans-serif)" is the default sans serif font: "Arial".
4. "(serif)" is the default serif font: "Times New Roman".
5. "(monospace)" is the default monospace font: "Consolas".
6. "r12a.io" is the PNG from Richard Ishida's UniView online app.
7. "glyphwiki.org" is the SVG from GlyphWiki. It looks a bit squashed because it's a half-width glyph; GlyphWiki is primarily concerned with CJK glyphs.
8. "unifont" is the GNU Unifont font. I couldn't find a webfont-friendly source for version 14, so I had to piggyback version 12 from Terence Eden.
9. "noto" is a composite font of several dozen Google Noto fonts. See ".noto" in universe.css.
10. Subsequent "Noto ..." glyphs are from the corresponding, individual Noto font, in priority order.

Universe 4: User Interface

The Universe character browser has a very basic user interface. In addition to the HTML5 presentation, there is a URL scheme that allows you to jump to various subpages.

Landing Page

universe.html#

The landing page gives a brief introduction and a collapsible table of statistics. As with all pages, a header contains breadcrumbs and a footer lists some useful jumping-off points.

Codepoints

To examine a specific codepoint, expressed in hexadecimal between "0000" and "10FFFF" inclusive, use:

universe.html#U+<hex>

In this case, "#U+0040" examines "@". The subpage lists the block, column and codepoint details, as well as font support, UCD data fields and external links, where appropriate.

Planes

To list all 17 Unicode planes, use:

universe.html#P

To examine details of the plane containing codepoint "U+<hex>", use:

universe.html#P+<hex>

Sheets

In this context, a "sheet" is a 32-by-32 grid of 1024 contiguous codepoints; it is how the Notoverse glyphs are organised.

To list all 161 sheets which contain allocated codepoints, use:

universe.html#S

To examine the sheet containing codepoint "U+<hex>", use:

universe.html#S+<hex>

Blocks

To list all 320 named Unicode blocks, use:

universe.html#B

To examine the block containing codepoint "U+<hex>", use:

universe.html#B+<hex>

This will list constituent codepoints, organised by column.

Columns

To examine just the column containing codepoint "U+<hex>", use:

universe.html#C+<hex>

This will list constituent codepoints in more detail.

Queries

To query the UCD for matching codepoints, use:

universe.html#<key>=<value>

The "<key>" can be:

• One of the abbreviated UCD field names, such as "gc" or "na".
• "id" to search the codepoint id (e.g. "U+0040").
• "basic" to search the computed codepoint basic category.
• "kind" to search the computed codepoint kind.
• "script" to search the codepoint script list (see below).
• "extra" to search NamesList.txt annotations.
• "text" to search all the above.

The "<value>" can be simple text or a JavaScript regular expression in the form "/<expr>/<flags>". For example:

universe.html#na=/\bANT\b/i

This searches for codepoints whose name field contains the whole word "ANT" case-insensitively.

Scripts

Queries with the special key "script" search the fields "sc" and "scx". To query for the 29 codepoints of the Ogham script, use:

universe.html#script=Ogam

List all the 210 scripts of the ISO-15924 standard, use:

universe.html#script

Search

Queries with the special key "search" perform full-text searches. To bring up a search dialog, use:

universe.html#search

Gears

As mentioned earlier, loading the full UCD database and glyph sheets for the first time can take quite a few minutes. Searches can also take a few seconds. For long-running JavaScript functions, we display animated gears:

To keep the page responsive, we wrap the long-running functionality inside a call to the "Gears()" function in universe.js:

function Gears(parent, asynchronous, complete) {

  var gears = document.createElement("img");

  gears.className = "gears";

  gears.title = "Please wait...";

  gears.src = "gears.svg";

  parent.appendChild(gears);

  gears.onload = async () => {

    var result = await asynchronous();

    if (gears.parentNode === parent) {

      parent.removeChild(gears);

    }

    if (complete) {

      complete(result);

    }

  };

}

Inside the asynchronous, long-running function we have to make sure we periodically call "YieldAsync()":

function YieldAsync(milliseconds) {

  // Yield every few milliseconds 

  // (or every time this function is called if argument is missing)

  var now = performance.now();

  if (!YieldAsync.already) {

    // First call

    YieldAsync.already = Promise.resolve(undefined);

    YieldAsync.channel = new MessageChannel();

  } else if (milliseconds && ((now - YieldAsync.previous) < milliseconds)) {

    // Resolve immediately

    return YieldAsync.already;

  }

  YieldAsync.previous = now;

  return new Promise(resolve => {

    YieldAsync.channel.port1.addEventListener("message",

      () => resolve(), { once: true });

    YieldAsync.channel.port1.start();

    YieldAsync.channel.port2.postMessage(null);

  });

}

This was inspired by a much-underrated StackOverflow answer.

Universe 3: Fonts

The Universe project uses Google Noto fonts as much as possible. As the Noto project page says:

The name is also short for "no tofu", as the project aims to eliminate 'tofu': blank rectangles shown when no font is available for your text.

According to the Universe Statistic page UCD 14.0.0, there are 144,762 "used" codepoints. This breaks down as follows when you include "unused" codepoints such as "private", "surrogate" and "noncharacter":

Kind	Criteria	Codepoints
format	gc is "Cf", "Zl" or "Zp"	165
control	gc is "Cc"	65
private	gc is "Co"	137,468
surrogate	gc is "Cs"	2,048
noncharacter	gc is "Cn"	66
modifier	gc is "Mc", "Me" or "Mn"	2,408
emoji	EPres is "Y"	1,185
graphic	otherwise	140,939
Total		284,344

Note that this "Kind" classification is slightly more fine-grained than Unicode's "basic type" but less so than "general category". Also note that the codepoints classified as "private", "surrogate" and "noncharacter" are fixed and will not change in subsequent Unicode versions.

This still leaves a great many codepoints that need to be rendered. The relationship between Unicode codepoints and character glyphs within a font is non-trivial, to say the least; but it can be useful, in a character browser, to render an "archetype" glyph of each codepoint for illustrative purposes.

In Universe, each "used" codepoint has a 32-by-32 pixel bitmap glyph. The aim is to use Google Noto fonts wherever possible to construct these bitmaps, because:

1. Noto fonts are "free and open source".
2. Their codepoint coverage is relatively good.
3. They try to adhere to a consistent look and feel.

Consequently, I named the set of bitmap glyphs "Notoverse". One can think of Notoverse as an alternative to GNU's Unifont initiative, except:

• The glyphs are 32-by-32, not 16-by-16.
• The glyphs are 24-bit RGB, not 1-bit monochrome.
• There is full Unicode 14.0.0 coverage.

The construction of the Notoverse glyphs was tedious and exhausting. I now know why so many similar projects run out of steam. The final breakdown of sources for each of the 144,762 glyphs is as follows:

• Hanazono: 58,118
• Google Noto (CJK): 43,937
• Google Noto (non-CJK): 34,225
• GlyphWiki: 4,948
• r12a.io UniView: 1,022
• BabelStone Khitan: 470
• Scraped from Unicode code charts: 346
• Manually constructed (including some Noto Emoji): 1,696

It turns out that Noto contributes to about 54% of the glyphs; more if we include the glyphs manually constructed from Noto elements.

U+0061: LATIN SMALL LETTER A

Here is the list of the Google Noto fonts I used (in priority order):

• Noto Sans
• Noto Sans Armenian
• Noto Sans Hebrew
• Noto Sans Arabic
• Noto Sans Syriac
• Noto Sans Thaana
• Noto Sans NKo/Noto Sans N Ko
• Noto Sans Samaritan
• Noto Sans Mandaic
• Noto Sans Malayalam
• Noto Sans Devanagari
• Noto Sans Bengali
• Noto Sans Gurmukhi
• Noto Sans Gujarati
• Noto Sans Oriya
• Noto Sans Tamil
• Noto Sans Tamil Supplement
• Noto Sans Telugu
• Noto Sans Kannada
• Noto Sans Malayalam
• Noto Sans Sinhala
• Noto Sans Thai
• Noto Sans Myanmar
• Noto Sans Georgian
• Noto Sans Cherokee
• Noto Sans Canadian Aboriginal
• Noto Sans Ogham
• Noto Sans Runic
• Noto Sans Tagalog
• Noto Sans Hanunoo
• Noto Sans Buhid
• Noto Sans Tagbanwa
• Noto Sans Khmer
• Noto Sans Mongolian
• Noto Sans Limbu
• Noto Sans Tai Le
• Noto Sans New Tai Lue
• Noto Sans Buginese
• Noto Sans Tai Tham
• Noto Sans Balinese
• Noto Sans Sundanese
• Noto Sans Batak
• Noto Sans Lepcha
• Noto Sans Ol Chiki
• Noto Sans Glagolitic
• Noto Sans Coptic
• Noto Sans Tifinagh
• Noto Sans Yi
• Noto Sans Lisu
• Noto Sans Vai
• Noto Sans Bamum
• Noto Sans Syloti Nagri
• Noto Sans PhagsPa
• Noto Sans Saurashtra
• Noto Sans Kayah Li
• Noto Sans Rejang
• Noto Sans Javanese
• Noto Sans Cham
• Noto Sans Tai Viet
• Noto Sans Ethiopic
• Noto Sans Linear A
• Noto Sans Linear B
• Noto Sans Phoenician
• Noto Sans Lycian
• Noto Sans Carian
• Noto Sans Old Italic
• Noto Sans Gothic
• Noto Sans Old Permic
• Noto Sans Ugaritic
• Noto Sans Old Persian
• Noto Sans Deseret
• Noto Sans Shavian
• Noto Sans Osmanya
• Noto Sans Osage
• Noto Sans Elbasan
• Noto Sans Caucasian Albanian
• Noto Sans Cypriot
• Noto Sans Imperial Aramaic
• Noto Sans Palmyrene
• Noto Sans Nabataean
• Noto Sans Hatran
• Noto Sans Lydian
• Noto Sans Meroitic
• Noto Sans Kharoshthi
• Noto Sans Old South Arabian
• Noto Sans Old North Arabian
• Noto Sans Manichaean
• Noto Sans Avestan
• Noto Sans Inscriptional Parthian
• Noto Sans Inscriptional Pahlavi
• Noto Sans Psalter Pahlavi
• Noto Sans Old Turkic
• Noto Sans Old Hungarian
• Noto Sans Hanifi Rohingya
• Noto Sans Old Sogdian
• Noto Sans Sogdian
• Noto Sans Elymaic
• Noto Sans Brahmi
• Noto Sans Kaithi
• Noto Sans Sora Sompeng
• Noto Sans Chakma
• Noto Sans Mahajani
• Noto Sans Sharada
• Noto Sans Khojki
• Noto Sans Multani
• Noto Sans Khudawadi
• Noto Sans Grantha
• Noto Sans Newa
• Noto Sans Tirhuta
• Noto Sans Siddham
• Noto Sans Modi
• Noto Sans Takri
• Noto Sans Warang Citi
• Noto Sans Zanabazar Square
• Noto Sans Soyombo
• Noto Sans Pau Cin Hau
• Noto Sans Bhaiksuki
• Noto Sans Marchen
• Noto Sans Masaram Gondi
• Noto Sans Gunjala Gondi
• Noto Sans Cuneiform
• Noto Sans Egyptian Hieroglyphs
• Noto Sans Anatolian Hieroglyphs
• Noto Sans Mro
• Noto Sans Bassa Vah
• Noto Sans Pahawh Hmong
• Noto Sans Medefaidrin
• Noto Sans Miao
• Noto Sans Nushu
• Noto Sans Duployan
• Noto Sans SignWriting
• Noto Sans Wancho
• Noto Sans Mende Kikakui
• Noto Sans Meetei Mayek/Noto Sans MeeteiMayek
• Noto Sans Adlam Unjoined
• Noto Sans Indic Siyaq Numbers
• Noto Serif Tibetan
• Noto Serif Vithkuqi
• Noto Serif Yezidi
• Noto Serif Ahom
• Noto Serif Dogra
• Noto Serif Tangut
• Noto Serif Hmong Nyiakeng/Noto Serif Nyiakeng Puachue Hmong
• Noto Sans Symbols
• Noto Sans Symbols2/Noto Sans Symbols 2
• Noto Sans Math
• Noto Sans Display
• Noto Looped Lao
• Noto Sans Lao
• Noto Sans CJK SC/Noto Sans SC
• Noto Music

Where there are two font names with a slash between them, the first is the local font name and the second the web font name. Alas, the naming is somewhat lax. See the HTML source and CSS for more details.

I hope I haven't trodden on anyone's toes by using their fonts in this way. The individual glyphs are down-sampled to 32-by-32 pixels and used for illustrative purposes only. I trust you'll agree that's "fair use".

So, it looks like we're still a long way from getting a pan-Unicode font, or even a set of fonts that achieve the same goal.

For completeness, here's a list of attempts at providing good Unicode coverage:

• Lucida Unicode, Microsoft, 1993
• Everson Mono, Michael Everson, 1995
• Code2000 et al, James Kass, 1998-2008
• GNU Unifont, 1998-
• GNU FreeFont, 2002-
• GlyphWiki, 2006-
• Google Noto, 2012-

Universe 2: Loading Resources

When the Universe web page first loads into a browser, about 100MB of data are pulled over the network in over 250 HTTP requests. This includes 77 web fonts (6MB), 161 glyph image sheets (77MB) and the Unicode Character Database, UCD, as a tab-separated value file (28MB).

It can take three or four minutes the first time around with a slow network connection, but all these resources are usually cached by the browser, so subsequent page loads perform very little actual data transfer. However, decoding the UCD is another matter.

Even the subset of the UCD data we're actually interested in takes up a quarter of a gigabyte when expressed as JSON. So caching the raw JSON file is problematic. I elected to transfer the data as sequential key-value deltas in TSV format. This reduces the size down to under 30MB and only 6.5MB when compressed "on the wire". It is also relatively quick to reconstitute the full UCD object hierarchy in JavaScript: it takes about seven seconds on my machine.

Here are the lines describing codepoint U+0040 ("@"):

na<tab>COMMERCIAL AT

lb<tab>AL

STerm<tab>N

Term<tab>N

SB<tab>XX

0040

<tab>= at sign

The first five lines (in "<key><tab><value>" form) list only the differences in UCD properties (keyed by short property aliases) compared to the preceding codepoint (i.e. U+003F "?").

The next line (in "<hex>" form) creates a new codepoint record for "U+0040".

The final line (in "<tab><extra>" form) adds an extra line of narrative to the preceding record. In this case, it refers to a NamesList.txt alias.

The ucd.14.0.0.tsv file is constructed using a NodeJS script from the following sources:

• ucd.all.flat.xml (194MB) from https://www.unicode.org/Public/UCD/latest/ucdxml/ucd.all.flat.zip
• https://www.unicode.org/Public/UCD/latest/ucd/NamesList.html (1.6MB)
• https://www.unicode.org/iso15924/iso15924.txt (13KB)

It is read and reconstituted by the "LoadDatabaseFileAsync()" function of universe.js. Notice that the final action of that function is to store the data in an IndexedDB database. This allows the JavaScript to test for the existence of that data in subsequent page reloads, obviating the need to fetch and decode each time. This saves several seconds each time. See "IndexedDatabaseGet()" and "IndexedDatabasePut()" in universe.js.

The downside of using this client-side caching is that it takes up 260MB of disk space:

We rely on the browser (Chrome, in this case) to manage the IndexedDB storage correctly, but even if the cache is purged, we fall back over to parsing the TSV again.

Universe 1: Introduction

Version 14.0.0 of Unicode was released back in September. There are an plethora of online resources for browsing the Unicode Character Database (UCD):

• Unicode Utilities: Character Properties
• r12a.io UniView
• GlyphWiki
• decodeunicode
• graphemica
• ScriptSource
• FileFormat.info
• Compart Unicode
  

But they usually have something lacking: the ability to render the codepoints and/or keeping up-to-date with the ever-evolving Unicode standard.

Of course, you can just download the official Unicode code charts as a single PDF and manually cross-reference them with the UCD. But the PDF is over 100MB and the UCD is distributed as a collection of human-unfriendly text files.

Universe is my attempt at producing a client-side HTML/CSS/JavaScript Unicode browser. It's obviously a work in progress, but the main areas of interest (that I plan to cover in subsequent blog posts) are:

1. A user interface to navigate around Unicode codepoints, blocks, planes, etc.
2. Loading the UCD into the client (this is my biggest concern at present as it takes about ten seconds to load and parse the database).
3. A flexible search mechanism.
4. Font support.
5. A representative rendering of all the codepoints.

Voronoi

I've just been baking. But what do you think of when you see the results?

1. Biscuits
2. Cookies
3. Voronoi

Depending on your answer:

1. You're probably British
2. You're probably American
3. You're definitely a geek

Machin Postage Stamps 3

I've done some investigation into Machin stamp designs that take into account colour vision deficiency (CVD). In particular, I looked at CVD-safe colour schemes and visual representation of numerals for the denominations. See those three web pages for more details.

The numeral scheme I finally came up with (after a lot of experimentation) is as follows:

The symbols have the following properties:

1. The number of small dots is the value of the digit.
2. Each has a high-contrast, CVD-safe colour (from the 'Chilliant Pale/Deep 19' palette).
3. The outlines are distinct.
4. They all fit within a circle the size of the grey ring zero.

For dark backgrounds, simply switch the pale/deep pairings:

The names I've ascribed to each of the symbols are:

• 0: grey ring
• 1: slate circle
• 2: brown oval
• 3: purple triangle
• 4: cyan cross
• 5: green bowtie
• 6: pink star
• 7: blue heptagon
• 8: orange square
• 9: mint lozenge

Daltonism

Machin stamps are colour-coded according to their denomination. The coding scheme is somewhat ad hoc. But what if we wanted to be more systematic?

There are surprising few existing systems for encoding numbers as colours. One is the old system used for electronic components:

The digits zero to nine are represented by ten colours. My favourite mnemonic is:

Black Bananas Really Offend Your Girlfriend, But Violets Get Welcomed

In the past, colour-blind people were allegedly discouraged from becoming electricians because of the possibility of confusing earth (green), live (red) and neutral (black) in the pre-1977 UK domestic mains cabling colour scheme.

In an ideal world, the mapping of colours to numeric values would be fairly immune to any colour vision deficiency (CVD) experienced by the viewer. This led me to an investigation into colour-blindness: what used to be called "Daltonism" in the UK.

There are plenty of resources on the web explaining the various forms of colour blindness, but I wanted to be able to objectively assess how "good" a palette of colours was for:

1. People with no colour deficiency (I'll call them "trichromats"),
2. People with protanopia, deuteranopia or tritanopia ("dichromats"), and
3. People with monochrome vision ("monochromats").

One metric of how well a palette of colours "fills" a colour space is to measure the minimum "distance" between any two entries. I chose the CIELAB colour space and the CIEDE2000 metric because they were close-at-hand as part of my previous Goldenrod project.

I defined lambda as the minimum distance (ΔE2000) between colours in the palette as seen by trichromats; also known as minD(normal). The greater this number, the less likely that two entries within the palette will be confused by trichromats.

I then used a corrected version of Color.Vision.Simulate from HCIRN to simulate the four colour deficiencies and produce four "confused" palettes from the original:

1. protanope
2. deuteranope
3. tritanope
4. achromatope

Each of the confused palettes will have a minimum distance between colours within them; call these minimum distances minD(protanope), etc.

I defined beta as the minimum of minD(protanope), minD(deuteranope) and minD(tritanope). The greater this number, the less likely that two entries within the original palette will be confused by dichromats. I appreciate that there are far fewer sufferers of tritanopia in the general population than of the other two forms of dichromatism, but I haven't scaled the three distance metrics accordingly; I'm running under the premise of "none left behind".

I defined alpha to be minD(achromatope). The greater this number, the less likely that two entries within the original palette will be confused by monochromats.

Finally, I defined omega to be the minimum distance between two adjacent CIELChab hues from the original palette, measured in degrees. This number measures hue separation perceived by trichromats.

In summary:

• Lambda, λ, is "min ΔE2000" for the original, trichromatic palette. It measures how different the colours in the palette seem to a viewer with no colour vision deficiency. Larger values indicate greater variation.
• Beta, β, is the least "min ΔE2000" for the dichromatic remappings of the palette. It measures how different the colours in the palette seem to a viewer with one of those colour vision deficiencies. Larger values indicate greater variation.
• Alpha, α, is "min ΔE2000" for the achromatic remapping of the palette. It measures how different the colours in the palette seem to a viewer with achromatopsia, when rendered in greyscale or in some low-light conditions. Larger values indicate greater variation.
• Omega, ω, is "min Δhab" for the original, trichromatic palette. It measures the perceived hue separation (measured in degrees) experienced by a viewer with no colour vision deficiency. Larger values indicate greater separation.

Unfortunately, as the number of entries in a palette increases, we expect the λ, β, α and ω scores to decrease, so we cannot easily compare palettes with differing numbers of entries. Perhaps the scores could be scaled depending on the palette size, but I haven't tried to work out the factor; I suspect it's not linear.

In general, for our purposes, a "good" palette is one with high λ, β and/or α scores. Maximising λ is appropriate for about 92% of the population; β for about 8%; and α for less than 0.01%.

The accompanying web page computes the scores for existing and novel palettes.

If we take "Chilliant Pale/Deep 19" from that page and re-order the palette into hue order, we get a colour-blind-friendly scheme with which to encode the digits zero to nine:

This could be the basis for a new colour-coding of stamp denominations...

Unicode Numeral Systems

As part of my investigations into Machin stamps, I started looking at numeral systems for labelling stamp denominations and also clock faces.

Unicode 13.0.0 contains a few General Categories used to classify code points according to numeric value ("Nd", "Nl" & "No") plus Derived Numeric Types ("Decimal", "Digit" & "Numeric"). Trawling through these and the Wikipedia pages on numeral systems, I came up with well over one hundred systems that can be used to represent numbers in Unicode using single glyphs:

Unicode Numerals web page

As it turns out, this experiment became more of an exercise in font management. I initially used Unifont for rendering, but this is quite ugly. The Code2000 fonts are no longer maintained. I ended up using Googles Noto fonts. However, there doesn't seem to be a definitive list of which glyphs exist in which font, so I had to create a tool to interrogate all the Noto web fonts I could find. Even an online list of those web fonts seems lacking, so here's one:

• Noto Kufi Arabic
• Noto Naskh Arabic
• Noto Naskh Arabic UI
• Noto Nastaliq Urdu
• Noto Sans
• Noto Sans JP
• Noto Sans KR
• Noto Sans SC
• Noto Sans TC
• Noto Sans Adlam
• Noto Sans Adlam Unjoined
• Noto Sans Anatolian Hieroglyphs
• Noto Sans Arabic
• Noto Sans Arabic UI
• Noto Sans Armenian
• Noto Sans Avestan
• Noto Sans Balinese
• Noto Sans Bamum
• Noto Sans Batak
• Noto Sans Bengali
• Noto Sans Bengali UI
• Noto Sans Bhaiksuki
• Noto Sans Brahmi
• Noto Sans Buginese
• Noto Sans Buhid
• Noto Sans Canadian Aboriginal
• Noto Sans Carian
• Noto Sans Chakma
• Noto Sans Cham
• Noto Sans Cherokee
• Noto Sans Coptic
• Noto Sans Cuneiform
• Noto Sans Cypriot
• Noto Sans Deseret
• Noto Sans Devanagari
• Noto Sans Devanagari UI
• Noto Sans Display
• Noto Sans Egyptian Hieroglyphs
• Noto Sans Ethiopic
• Noto Sans Georgian
• Noto Sans Glagolitic
• Noto Sans Gothic
• Noto Sans Gujarati
• Noto Sans Gujarati UI
• Noto Sans Gurmukhi
• Noto Sans Gurmukhi UI
• Noto Sans Gunjala Gondi
• Noto Sans Hanifi Rohingya
• Noto Sans Hanunoo
• Noto Sans Hebrew
• Noto Sans Imperial Aramaic
• Noto Sans Indic Siyaq Numbers
• Noto Sans Inscriptional Pahlavi
• Noto Sans Inscriptional Parthian
• Noto Sans Javanese
• Noto Sans Kaithi
• Noto Sans Kannada
• Noto Sans Kannada UI
• Noto Sans Kayah Li
• Noto Sans Kharoshthi
• Noto Sans Khmer
• Noto Sans Khmer UI
• Noto Sans Khudawadi
• Noto Sans Lao
• Noto Sans Lao UI
• Noto Sans Lepcha
• Noto Sans Limbu
• Noto Sans Linear B
• Noto Sans Lisu
• Noto Sans Lycian
• Noto Sans Lydian
• Noto Sans Malayalam
• Noto Sans Malayalam UI
• Noto Sans Mandaic
• Noto Sans Masaram Gondi
• Noto Sans Mayan Numerals
• Noto Sans Medefaidrin
• Noto Sans MeeteiMayek
• Noto Sans Mende Kikakui
• Noto Sans Meroitic
• Noto Sans Modi
• Noto Sans Mongolian
• Noto Sans Mono
• Noto Sans Mro
• Noto Sans Myanmar
• Noto Sans Myanmar UI
• Noto Sans New Tai Lue
• Noto Sans Newa
• Noto Sans Ogham
• Noto Sans Ol Chiki
• Noto Sans Old Italic
• Noto Sans Old Persian
• Noto Sans Old South Arabian
• Noto Sans Old Turkic
• Noto Sans Oriya
• Noto Sans Oriya UI
• Noto Sans Osage
• Noto Sans Osmanya
• Noto Sans Pahawh Hmong
• Noto Sans Phags Pa
• Noto Sans Phoenician
• Noto Sans Rejang
• Noto Sans Runic
• Noto Sans Samaritan
• Noto Sans Saurashtra
• Noto Sans Sharada
• Noto Sans Shavian
• Noto Sans Sinhala
• Noto Sans Sinhala UI
• Noto Sans Sundanese
• Noto Sans Syloti Nagri
• Noto Sans Symbols
• Noto Sans Symbols 2
• Noto Sans Syriac
• Noto Sans Tagalog
• Noto Sans Tagbanwa
• Noto Sans Tai Le
• Noto Sans Tai Tham
• Noto Sans Tai Viet
• Noto Sans Takri
• Noto Sans Tamil
• Noto Sans Tamil UI
• Noto Sans Telugu
• Noto Sans Telugu UI
• Noto Sans Thaana
• Noto Sans Thai
• Noto Sans Thai UI
• Noto Sans Tifinagh
• Noto Sans Tirhuta
• Noto Sans Ugaritic
• Noto Sans Vai
• Noto Sans Wancho
• Noto Sans Warang Citi
• Noto Sans Yi
• Noto Serif
• Noto Serif JP
• Noto Serif KR
• Noto Serif SC
• Noto Serif TC
• Noto Serif Ahom
• Noto Serif Armenian
• Noto Serif Bengali
• Noto Serif Devanagari
• Noto Serif Display
• Noto Serif Ethiopic
• Noto Serif Georgian
• Noto Serif Gujarati
• Noto Serif Hebrew
• Noto Serif Kannada
• Noto Serif Khmer
• Noto Serif Lao
• Noto Serif Malayalam
• Noto Serif Myanmar
• Noto Serif Nyiakeng Puachue Hmong
• Noto Serif Sinhala
• Noto Serif Tamil
• Noto Serif Telugu
• Noto Serif Thai
• Noto Serif Tibetan

The Font Check tool allows you to type in a hexadecimal Unicode code point and see the fonts that can render it. It uses the trick of measuring the glyph using an offscreen canvas with a fallback font of Adobe Blank. If the glyph is zero pixels wide, it means it was rendered using the fallback (or is naturally zero-width, so isn't of interest to us anyway).

Using the tool, I worked out the minimal set of Noto fonts needed to render the numerals table. However, there were a few issues:

1. Some fonts only come in serif variants, not sans serif (and vice versa).
   
   
2. I couldn't find any Noto web fonts that could render the following (though the asterisked scripts were rendered correctly using a fallback font by my browser):
   
   
• Dives Akuru
• Khmer Divination*
• Myanmar Tai Laing*
• Nko*
• Ottoman Siyaq
• Sinhala*
• Sora Sompeng*
• Tag
  
  
3. Arabic Persian and Arabic Urdu use exactly the same codepoints but use different languages in the HTML mark-up to select different sets of glyphs.

Further notes:

• I couldn't find any information on how Ogham represented numbers, so I made something up based on tally marks.
• The Tibetan script has a parallel set of numerals for half values; they're used in stamps, which is a nice coincidence.
• The Runic Golden Numbers are used in Younger Futhark calendars.
• Other scripts do have numerals or counting systems, but I excluded many because they are "low radix" (e.g. native Korean)

Machin Postage Stamps 2

Well, I thought I was being clever, didn't I? Using WebP images for Machin stamps. Alas, WebP has only recently been supported by Apple's Safari, so the web page didn't work at all on an older model iPad.

My original HTML was simply:

<img id="picture" class="shadow" src="machin.webp" />

And the source image path was accessed from JavaScript via:

document.getElementById("picture").src

The fix from Brett DeWoody is actually quite elegant. Change the HTML to use picture source sets:

<picture class="shadow">

    <source srcset="machin.webp" type="image/webp" />

    <img id="picture" src="machin.png" />

</picture>

And use the following to interrogate the chosen path after load:

document.getElementById("picture").currentSrc

Machin Postage Stamps 1

There is a web page to accompany these blog posts.

I was sorting through some old family papers when I came across my father's stamp collection. He had a number of unsorted UK stamps that I (being me) decided to organise.

Arnold Machin

The Machin series of UK postage stamps are named after the sculptor (Arnold Machin, 1911-1999) who designed them. His profile of Queen Elizabeth II has been used on many coins and stamps:

Pre-Decimal Machin Stamps

The original, pre-decimal stamps to use the Machin profile (from 1967 onwards) came in denominations of:

½d, 1d, 2d, 3d, 4d, 5d, 6d, 7d, 8d, 9d, 10d, 1/-, …

Each denomination had a different colour, although I'm fairly certain there was no systematic colour scheme.

I found all of the denominations, up to and including the shilling, in my father's collection, so I thought about how to mount them in a display. These stamps aren't very valuable, so permanently sticking them to a bit of card isn't so terrible.

My first thought was just a grid:

Or perhaps a circular layout:

At this point, I was reminded of a clock face. Alas, there was never a "11d" Machin stamp, but one could swap the half penny and shilling stamps and use "½d" for eleven o'clock and "1/-" for twelve o'clock:

Here's a mock-up of a clock built around this layout:

I also built a JavaScript demo loosely based on a beautiful CSS-only clock by Nils Rasmusson.

Decimal Machin Stamps

Next I moved on to the Machin stamps used after decimalisation in 1971. These had all the half-penny increments up to and including 13½p, so two rings could be constructed:

Or, with axis-aligned stamps:

These templates are available on the web page as SVGs with absolute measurements: each stamp is 21mm by 24mm. You can print out the desired page at 100% scale and use the templates when mounting the stamps. Unfortunately the "double ring" layouts don't quite fit on a single sheet of A4 so you'll need to crop and rely on symmetry to physically flip the template.

Mounting

I decided to mount 23 stamps (my father never acquired a "11½p" Machin) using the last template within a 240mm-by-300mm frame:

1. Print out the template at 100% scale.
2. Carefully cut along three sides of each stamp "window" with a scalpel.
3. Position the template over the mounting card.
4. Secure the template to the mounting card with masking tape. Try to avoid sticking the tape directly to the front of the card. (Figure 1)
5. Stick the appropriate stamps on to the card using double-sided tape through the windows. (Figure 2)
6. Carefully remove the template and insert the mounting card into the frame. (Figure 3)

Figure 1

Figure 2

Figure 3

There's a conspicuous gap where the missing stamp should go. I could fill it by splurging a couple of quid on ebay, but the gap itself has a story.

Another project would be to affix a cheap battery quartz movement to a similar clock face. I had hoped to use an old CD for the circular face, but I don't think twelve stamps quite fit.

Gratuitous Aphorism #8

Experts are just people who have already made all the silly mistakes.

Hexworld 3: Compression

Last time, we encoded our 311,040 world map hexel indices as a 622,080-character hexadecimal string as a way of embedding the data in an ASCII JavaScript file. We could use the following script:

hexworld(buffer => {

  const DATA = "00000000...ffffffff";

  buffer.set(DATA.match(/../g).map(x => parseInt(x, 16)));

});

This calls a function hexworld(), defined elsewhere, that takes as its only parameter a decompression function that fills in a pre-allocated Uint8Array buffer with the hexel indices. The "decompression" above consists of splitting the long hexadecimal string into 2-character segments and converting these to numeric values.

We can achieve better compression by using the built-in atob() function:

hexworld(buffer => {

  const DATA = "AAAAAAAA...////////";

  buffer.set(Array.from(atob(DATA), x => x.charCodeAt()));

});

The DATA string is reduced in size from 622,080 ASCII characters to 414,720.

If we look at the map itself, we see that it's ripe for run-length encoding or the like.

One possibility is the LZW compression algorithm. I tried this and came up with data plus decompressor what weigh in at under 32KB of ASCII:

function lzw(src) {

  var dic = Array.from({ length: 256 }, (_, i) => [i]);

  var key, dst = [];

  for (var val of src) {

    var nxt = dic[val] || [...key, key[0]];

    if (key) {

      dic.push([...key, nxt[0]]);

    }

    key = nxt;

    dst.push(...key);

  }

  return dst;

}

hexworld(buffer => {

  const DATA = "00007407...cb8cc80f";

  buffer.set(lzw(DATA.match(/.../g).map(x => parseInt(x, 36))));

});

The lzw() function above decompresses an array of integers into an array of bytes. For completeness, here's the corresponding compression function:

function compress(src) {

  const chr = String.fromCharCode;

  var dic = {};

  var idx = 0;

  do {

    dic[chr(idx)] = idx;

  } while (++idx < 256);

  var dst = [];

  var pre = "";

  for (var val of src) {

    var key = pre + chr(val);

    if (key in dic) {

      pre = key;

    } else {

      dst.push(dic[pre]);

      dic[key] = idx++;

      pre = chr(val);

    }

  }

  dst.push(dic[pre]);

  return dst;

}

In our Hexworld case, the LZW dictionary constructed during compression has about 10,000 entries, so those indices can be stored as three base-36 digits. This is a general-purpose compression scheme, so could a more tailored algorithm produce better results? Remember, we're aiming for something less than 16KB.

One solution I looked at was encoding the data as a sequence of 4-bit nybbles:

hexworld(buffer => {

  const DATA = "8bxQEhER...ER8NEw==";

  var input = Array.from(atob(DATA),

    x => x.charCodeAt().toString(16).padStart(2, "0")).join("");

  var i = 0;

  function read(n) {

    i += n;

    return parseInt(input.slice(i - n, i), 16);

  }

  var land = 0;

  var next = 0;

  var o = 0;

  while (o < buffer.length) {

    var n = read(1);

    switch (n) {

      case 0:

        land = next = read(2);

        continue;

      case 12:

        n = read(1) + 12;

        break;

      case 13:

        n = read(2) + 28;

        break;

      case 14:

        n = read(3) + 284;

        break;

      case 15:

        n = read(4) + 4380;

        break;

    }

    buffer.fill(next, o, o + n);

    o += n;

    next = next ? 0 : land;

  }

});

The algorithm is as follows:

1. Read the next nybble in the stream
2. If the nybble is 0, the next two nybbles contain the next "land" hexel index and go back to Step 1
3. If the nybble is between 1 and 11 inclusive, it is used as the count below
4. If the nybble is 12, the count to use is the value in the next nybble plus 12
5. If the nybble is 13, the count to use is the value in the next two nybbles plus 28
6. If the nybble is 14, the count to use is the value in the next three nybbles plus 284
7. If the nybble is 15, the count to use is the value in the next four nybbles plus 4380
8. If the last set of values output were "land", write out "count" indices of "water" (0)
9. Otherwise, write out "count" indices of the current "land"
10. Go back to Step 1

This algorithm assumes there are never more than about 70,000 value repetitions, which is more than enough for our map. It weighs in at under 19KB of ASCII text, which is getting very close to our goal. One thing to notice is that the nybbles are encoded into ASCII via atob/btoa which use base-64 and are therefore relatively inefficient.

My final attempt (the one that achieved my goal of data plus decompressor within 16KB of ASCII) uses base-95:

hexworld(buffer => {

  const DATA = ')  )gD}l...$)wA#).n';

  for (var d = Array.from(DATA, x => 126 - x.charCodeAt()),

    i = 0, o = 0, a = 0, b = 0, c = 0; DATA[i]; c = c ? 0 : a) {

    var v = d[i++];

    if (v >= 90) {

      v -= 88;

      while (--v) {

        d[--i] = 0;

      }

    }

    var n = ~~(v / 5);

    if (v %= 5) {

      c = v---4 ? v * 95 + d[i++] : b;

      b = a;

      a = c; 

    }

    switch (n++) {

      case 17:

        n = d[i++] * 95 + 112;

      case 16:

        n += d[i++] - 1;

        break;

    }

    buffer.fill(c, o, o + n);

    o += n;

  }

});

This is slightly golfed, so I'll clarify it below.

[In a perverse way, I quite like the expression "v---4" which is shorthand for "(v--) !== 4"]

The data is encoded in base-95: the number of printable ASCII characters. This means that backslashes and quotes need to be escaped within the string. The choices of (a) using single quotes (as opposed to double- or backquotes) and (b) storing values in reverse order ("126 - x" versus "x - 32") minimize the number of escape backslashes needed for our particular map data.

Lead base-95 values are split into two values: low (0 to 4 inclusive) and high (0 to 18 inclusive). The high value holds the repetition count:

• High values from 0 to 15 inclusive imply repetition counts from 1 to 16,
• Sixteen takes the next base-95 value to produce a repetition counts from 17 to 111,
• Seventeen takes the next two base-95 values to produce a repetition counts from 112 to 9136,
• Eighteen is a special "repeated zero" value that simulates a lead zero repeated 2 to 6 times based on the low value.

The low value (except for when the high value is eighteen) encodes what should be repeated:

• Zero alternates between the last land index and the water index (0),
• One sets the land index to the next base-95 value,
• Two sets the land index to the next base-95 value plus 95,
• Three sets the land index to the next base-95 value plus 190,
• Four alternates between the last land index and the previous land index specified.

This rather ad hoc algorithm is based on the following observations:

1. Water (hexel index zero) is common throughout the whole map,
2. If the last land hexel was a particular index, it is likely that the next land will be the same index,
3. Due to the staggered hexel layout, land indices quite often alternate with either water or the previous land index

I'm sure there's plenty more mileage using bespoke compression, but after a certain point it becomes unhealthy. For example, one option I didn't pursue is re-ordering the country-to-hexel index allocation in order to improve compression. This smells suspiciously like super-optimisation.

One last avenue to explore for compressing the hexel map is the recent JavaScript Compression Stream API, but that's for another time.

Hexworld 2: Encoding

As mentioned in the first part, the map of Hexworld consists of a 864-by-360 staggered grid of hexagons. Each hexagon (hexel) holds an 8-bit index, so the whole thing fits into about 300KB of binary data. It can be stored as an 8-bit PNG weighing in at about 13½KB:

Greyscale optimisations and PNG Crush will reduce this to about 11½KB. However, reading the pixel index values back using JavaScript so that we can reconstruct the hexel data is problematic. One would think you could simply do the following:

• Encode the greyscale PNG as a data URL,
• Load it into an offscreen img element,
• Draw it into an offscreen canvas element, 
• Capture the pixel data via getImageData() element, then
• Reconstruct the indices.

The two main stumbling blocks are:

1. Loading images (even data URLs) is an asynchronous activity.
2. Colour space management typically applied a "gamma" correction which means the greyscale RGB values are not one-to-one with the original indices.

The first problem can be solved with some truly horrific fudging:

  var done = false;

  img.onload = () => {

    process(img);

    done = true;

  };

  img.src = dataURL;

  while (!done) {

    await new Promise(r => setTimeout(r, 100));

  }

The second issue cannot be solved without using a third-party JavaScript library (like pngjs) to decode the raw PNG data and extracting the indices directly.

Another option is to encode the raw pixel data (as opposed to the PNG) into the JavaScript script itself. For example:

  function decode_hex(buffer) {

    const HEXWORLD = /* hexadecimal string */;

    buffer.set(HEXWORLD.match(/../g).map(x => parseInt(x, 16)));

  }

This function takes a 311,040-element Uint8Array (that's 864 times 360) as an argument and fills it with the indices. Unfortunately, the hexadecimal string is over 600,000 characters long!

If we limit ourselves to ASCII JavaScript, can we do better?