Unicode Trivia U+0F33

Codepoint: U+0F33 "TIBETAN DIGIT HALF ZERO"
Block: U+0F00..0FFF "Tibetan"

The Unicode Character Database has a field named "Numeric_Value" (abbreviated to "nv"). For the vast majority of the 144,697 used codepoints in Unicode 14.0.0 (in fact, precisely 142,890) this field holds the value "NaN" meaning that the codepoint does not represent a numeric value.

Other values for "nv", with the number of codepoints having that value in parentheses, are shown below, in approximate order of frequency.

First, the denary digits. The distribution is not flat because of the irregularity of CJK ideographs representing small numbers and the lack of a "zero" digit in some writing systems:

• "1" (141)
• "2" (140)
• "3" (141)
• "4" (132)
• "5" (130)
• "6" (114)
• "7" (113)
• "8" (109)
• "9" (113)
• "0" (84)

Next, multiples of ten:

• "10" (62)
• "20" (36)
• "30" (19)
• "40" (18)
• "50" (29)
• "60" (13)
• "70" (13)
• "80" (12)
• "90" (12)

Next, powers of ten. Characters for trillions are using in Japan and Taiwan (U+5146) and in the Pahawh Hmong script (U+16B61):

• "100" (35)
• "1000" (22)
• "10000" (13)
• "100000" (5)
• "1000000" (1)
• "10000000" (1)
• "100000000" (3)
• "10000000000" (1)
• "1000000000000" (2)

Next, sequential values up to twenty:

• "11" (8)
• "12" (8)
• "13" (6)
• "14" (6)
• "15" (6)
• "16" (7)
• "17" (7)
• "18" (7)
• "19" (7)

Next, blocks of circled numbers:

• "21" (1)
• "22" (1)
• "23" (1)
• "24" (1)
• "25" (1)
• "26" (1)
• "27" (1)
• "28" (1)
• "29" (1)

• "31" (1)
• "32" (1)
• "33" (1)
• "34" (1)
• "35" (1)
• "36" (1)
• "37" (1)
• "38" (1)
• "39" (1)

• "41" (1)
• "42" (1)
• "43" (1)
• "44" (1)
• "45" (1)
• "46" (1)
• "47" (1)
• "48" (1)
• "49" (1)

Next, multiples of 100. We can see the importance of 500 in ancient counting systems (e.g. "D" in Roman numerals)

• "200" (6)
• "300" (7)
• "400" (7)
• "500" (16)
• "600" (7)
• "700" (6)
• "800" (6)
• "900" (7)

Next, multiples of 1000:

• "2000" (5)
• "3000" (4)
• "4000" (4)
• "5000" (8)
• "6000" (4)
• "7000" (4)
• "8000" (4)
• "9000" (4)

Next, multiples of 10,000:

• "20000" (4)
• "30000" (4)
• "40000" (4)
• "50000" (7)
• "60000" (4)
• "70000" (4)
• "80000" (4)
• "90000" (4)

Next, multiples of 100,000 (e.g. "lakh"):

• "200000" (2)
• "300000" (1)
• "400000" (1)
• "500000" (1)
• "600000" (1)
• "700000" (1)
• "800000" (1)
• "900000" (1)

Next, multiples of 10,000,000 (e.g. "crore"):

• "20000000" (1)

Next are two large numbers from cuneiform (base 60):

• "216000" (1)
• "432000" (1)

Next, we start the rational fractions (e.g. "half"):

• "1/2" (18)

Next, the quarters:

• "1/4" (13)
• "3/4" (8)

Next, the eighths:

• "1/8" (7)
• "3/8" (1)
• "5/8" (1)
• "7/8" (1)

Next, the sixteenths:

• "1/16" (6)
• "3/16" (5)

Next, the thirty-seconds:

• "1/32" (1)

Next, the sixty-fourths:

• "1/64" (1)
• "3/64" (1)

Next, the thirds (strangely, there's an Ancient Greek "⅔" U+10177, but not for "⅓"):

• "1/3" (5)
• "2/3" (6)

Next, the fifths:

• "1/5" (3)
• "2/5" (1)
• "3/5" (1)
• "4/5" (1)

Next, the sixths:

• "1/6" (3)
• "5/6" (2)

Next, a seventh:

• "1/7" (1)

Next, a ninth:

• "1/9" (1)

Next, the twelfths (Meroitic cursive fractions, not reduced):

• "1/12" (1)
• "2/12" (1)
• "3/12" (1)
• "4/12" (1)
• "5/12" (1)
• "6/12" (1)
• "7/12" (1)
• "8/12" (1)
• "9/12" (1)
• "10/12" (1)
• "11/12" (1)

Next, a collection of (mostly Tamil and Malayalam) fractions we've seen already:

• "1/320" (2)
• "1/160" (2)
• "1/80" (1)
• "1/40" (2)
• "3/80" (2)
• "1/20" (2)
• "1/10" (3)
• "3/20" (2)

Finally, a collection of what can only be described as "strange halves":

• "3/2" (1)
• "5/2" (1)
• "7/2" (1)
• "9/2" (1)
• "11/2" (1)
• "13/2" (1)
• "15/2" (1)
• "17/2" (1)
• "-1/2" (1)

These last nine all belong to the "Tibetan / Digits minus Half" group of codepoints (U+0F2A to U+0F33), including the wonderfully perplexing U+0F33 "TIBETAN DIGIT HALF ZERO".

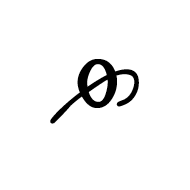[source]

This character supposedly has a numeric value of "-1/2" or "-0.5", and is the only codepoint (so far) with a negative "nv".

As Andrew West points out, there is much confusion (and little evidence) surrounding the numeric values of these codepoints. The glyphs seem to appear on postage stamps, but if the Royal Mail was in the habit of issuing stamps with a denomination of minus ½p, they quickly go out of business. If you went into a Post Office and asked for one million "-½p" stamps, the teller would be obliged to give you a huge tome of stamps and £5,000.